How to Calculate Shear Stress at a Point in a Bending Truncated Cone?

[Stanislavs]

Dear Colleagues,

This problem causes me a headache - any suggestions?

I have a truncated cone under bending on two axes.
I take a section where I have two acting side forces - Qx & Qy
I want to find shear stresses acting in the point A which is on a circumstance of the section 45° between axes X and Y. I independently calculate sheer stress from force Qx -> τx and Qy -> τy. The resultant shear force will be τxy.

On the other hand, I can in the begging take the resultant side force of Qx & Qy -> Qxy.
The direction of this force will be 45° to axes X and Y.
In this case there will be no shear stress at point A

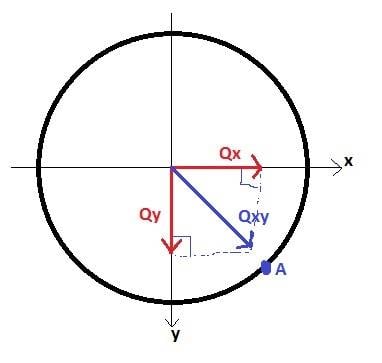
So which assumption is correct? Why are these different?

 

[Chestermiller]

The shear forces don't just act at the center of the cross section. There are distributed over the entire cross section. So the shear stress at A won't be zero. Also, unless Qx = Qy, the direction of the resultant shear stress will not be at 45 degrees.

Chet

 

[Stanislavs]

The shear forces don't just act at the center of the cross section. There are distributed over the entire cross section. So the shear stress at A won't be zero. Also, unless Qx = Qy, the direction of the resultant shear stress will not be at 45 degrees.

Chet

Yes, forgot to mention, in my case Qx = Qy.

The shear force (say Qx) is a sum (integral) of all distributed shear stresses in the section in this (x) direction.
The distributions of these shear stresses is as follows - max in the centre and 0 in the furthest point of cross section along direction x.
(http://www.nptel.ac.in/courses/Webcourse-contents/IIT-ROORKEE/strength%20of%20materials/lects%20&%20picts/image/lect28%20and%2029/lecture%2028%20and%2029.htm)

Am I wrong?

The tricky bit is if I can substitute Qx & Qy with resultant Qxy and if so, why there's such a difference in result?
In case of Qx & Qy - in point A there should be shear stress present, however if I substitute Qx & Qy I get Qxy and point A in this case is the very end of the section in the direction where side force Qxy is pointing.

 

[Chestermiller]

If you want to know the resultant stress at a point, you need to use the distributed stress at that point.

Chet

 

[Stanislavs]

Ok, just found this might fall under "unsymmetrical bending", when bending moment and shear force is not acting along principal axis.
In this case It's suggested that moment (presumably shear force as well) should be split into two components acting along principal axis and both cases should view separately and then combined.
Meaning I have to stick with Qx and Qy separately and there will shear stress at point A.

My question now is why I can't rotate principal axis of a circle if remains symmetrical?

 

[Chestermiller]

Ok, just found this might fall under "unsymmetrical bending", when bending moment and shear force is not acting along principal axis.
In this case It's suggested that moment (presumably shear force as well) should be split into two components acting along principal axis and both cases should view separately and then combined.
Meaning I have to stick with Qx and Qy separately and there will shear stress at point A.

My question now is why I can't rotate principal axis of a circle if remains symmetrical?

Sorry, I have no idea what you are asking.

Chet

 

[Stanislavs]

Ok, Here's everything in detail.
Please find attached shear stress distribution along Y axis due to side force Qy (don't pay attention to blue arrows yet)
Based on this, there is a shear stress τx acting on the line (marked red).
Point A (see previous pictures) belongs to this line, therefore if we consider point A as a small area dS, the shear force acting in this are will be τx.
The same goes for side force Qx (shear stress - marked blue)
Do we agree up until now?

Now what I was suggesting is replacing both forces Qx and Qy with resultant force Qxy (due to Qx = Qy, it'll be acting 45° between axis X and Y)
The shear force distribution along this ONE force should be similar, meaning there should be no shear force at point A (since it's the most far point along force Qxy)

What I'm saying now is that there is situation called "unsymmetrical bending" - when bending moment is not acting along one of the axis of symmetry (principal axis)
In reality it would look as if you replace my circle with "H" shape section and assign load acting 45° (the same as previously discussed force Qxy)
In this case it's suggested to split this force Qxy into two components along axis of symmetry (principal axis) - in my case these would be Qx and Qy calculate as if in my first example.

The question is why my case with "O" section is to be considered as asymmetrical bending?

 

[Chestermiller]

Still don't get it. Maybe it would help if you could represent the shear stresses as a function of x and y analytically.

Chet

 

[SteamKing]

I think the problem here is that any axis drawn thru the center is a principal axis for a beam with a circular cross section.

Also, when I dabbled a bit at studying elasticity, it was always assumed that the shear stress on the outer perimeter of a cross section was equal to zero (something about there being no tractive forces present there.)

The OP mentioned in his first post that he had a "truncated cone" which was undergoing bending. This implies to me that the beam is non-prismatic, hence the distribution of stresses along its length will be more complicated than for the prismatic beam.

I also believe if you are calculating τ = VQ / I t, then the shear force V (or its resultant) must act parallel to the axis of the section about which Q and I are calculated. For circular cross sections, I is the same regardless of axis orientation, and Q = 0 at the outer fiber of the cross section.

 

[Stanislavs]

Dear Chet,

Ok, I'll simplify the problem.
You have a beam fixed with one end to the ground with a cross section along the beam of a circle with a radius r = 1 m
There are two forces acting at the free end of the beam perpendicular to the length of the beam Qx = Qy = 200 N (end perpendicular between themeselves obviously)
Have to calculate shear stress at point A that's located on the sircumfurance of the end section at angle 45° (as in my previous cases)

Do I calculate these independantly for Qx and Qy (meaning firstly I calculate shear stres at point A as if only force Qx is present, then as if only force Qy is present; then sum up the vectors) or do I make a resultant force Qxy (sum of these vectors with value = square root of (Qx² + Qy²) ) and calculate it for this case?
You obviously get the different results. At least I do.

Dear SteamKing,

You're close to the point.
How the shear stress is distributed along the lentgth is not that inportant realy.
Regarding the formula - you are absolutally correct, that's the formula I use however Q in this formula is the side force itself (integral of all shear stress along the surface) and it's a constant. As for shear stresses - it's the same for all points that are located at the same distance

 

[SteamKing]

Do I calculate these independantly for Qx and Qy (meaning firstly I calculate shear stres at point A as if only force Qx is present, then as if only force Qy is present; then sum up the vectors) or do I make a resultant force Qxy (sum of these vectors with value = square root of (Qx² + Qy²) ) and calculate it for this case?
You obviously get the different results. At least I do.

While it's nice having this discussion, since you have an actual problem you have attempted to solve, why not post your calculations, so we can see what you are doing?

 

[Stanislavs]

My problem is more complicated - it has all bunch of load (bending, torsion, compression/tension) and I have to find the critical point (where crack will appear) and calculate stress at this point.
But I don't want to complicate things - the problem is exactly as I mentioned above.

SteamKing, actually you can transform that formula into:

This is a specific case for the circle cross-section.
As you can see shear stress depends in the side force as well as on the distance x from the center point along the Qx.
If x = d/2 = r (meaning the point is on the circumference), then the result will be 0.
Say I have two equal forces Qx and Qy acting perpendicular.
At point A (as usual) I would have distance x and y for the formula = r * cos45°
As a result I would have some shear stress value in X and in Y direction.

HOWEVER, if I substitute Qx and Qy with a resultant force Qxy = sqrt(Qx^2 + Qy^2), I will have instead of "x" value r or d/2.
However, if I insert d/2 in the formula instead of the x I will have 0 in the bracket and as a result τ will be 0.
So why is it 0 if in the previous case I got τx and τy not 0? And a resultant of those two will not be 0 also

 

[Chestermiller]

I'm totally confused. The equation you gave for τ_x should integrate over the area to Q_x. But, it doesn't, because it is not even dimensionally consistent with such an integration. Secondly, you say that, at point A, x = d/2 , τ_x is equal to zero. But this is not correct. At point A, $x = \frac{1}{\sqrt{2}}\frac{d}{2}$. So τ_x is not zero there. It is hard to discuss this situation further until the functional relation describing the shear stress distribution is confidently specified.

I would also like to point out that, since this is a linear situation, the solutions with regard to x should linearly superimpose with the solutions with regard to y.

Chet

 

[Stanislavs]

Ok, I've gathered everything in my picture (see link).
The first part is how I calculate shear stress out of side force (how I get the formula)
The second part - two approaches to finding shear stress at point A.
Why the results are different and WHY?

If even this doesn't clarify my question, I give up - we're clearly talking about different worlds...

http://postimg.org/image/npnr0e1wb/

http://postimg.org/image/npnr0e1wb/

 

[Chestermiller]

Ok, I've gathered everything in my picture (see link).
The first part is how I calculate shear stress out of side force (how I get the formula)
The second part - two approaches to finding shear stress at point A.
Why the results are different and WHY?

If even this doesn't clarify my question, I give up - we're clearly talking about different worlds...

http://postimg.org/image/npnr0e1wb/

[PLAIN]http://postimg.org/image/npnr0e1wb/[/QUOTE]
As best I can tell, what you are saying is:

$$τ_y=Q_yf(y)$$
$$τ_x=Q_xf(x)$$

where $f(ξ)=\frac{4}{3A}\left(1-\left(\frac{2ξ}{d}\right)^2\right)$, with ξ representing a dummy variable. So,

$$τ=\sqrt{τ_y^2+τ_x^2}=\sqrt{Q_y^2f^2(y)+Q_x^2f^2(x)}$$
But, I think you are also trying to say that:
$$τ=\sqrt{Q_y^2+Q_x^2}f(\sqrt{x^2+y^2})$$
But, the latter is just not correct algebraically.

If I'm misunderstanding, I apologize.

Chet

 

[SteamKing]

Ok, I've gathered everything in my picture (see link).
The first part is how I calculate shear stress out of side force (how I get the formula)
The second part - two approaches to finding shear stress at point A.
Why the results are different and WHY?

If even this doesn't clarify my question, I give up - we're clearly talking about different worlds...

http://postimg.org/image/npnr0e1wb/

I'm not going to try to work thru your integrations ... it's much easier to look up circular segments and find the necessary data:

http://mathworld.wolfram.com/CircularSegment.html

Q for the segment is then the product of the area and its centroid, thus:

Q = A * y-bar

A = (R²/2)*(θ - sin θ)

y-bar = 4R*sin³(θ/2) / [3(θ - sin θ)]

where

R = radius of the circle
θ = central angle of the segment

Thus Q = (2R³/3) * sin³(θ/2)

The shear stress τ = VQ / I t , where

I = πR⁴ / 4

t = length of the base of the circular segment = 2R sin (θ/2)

so combining it all,

τ = V * (Q / I t), where V = shear force

Q / I t = [1/(3πR²)] * sin²(θ/2) or

τ = V * [1/(3πR²)] * sin²(θ/2)

In this calculation, the shear stress τ is located at the base of the circular segment, not on the perimeter of the circle.

 

[Stanislavs]

Dear Chet,

The equations provided by you fully sums up the idea
So the dilemma I have is which one of these approaches is correct?
Is there a reason I can't substitute both side forces by one?

 

[Chestermiller]

Hi Stanislavs,

I'm relieved to hear that I was finally able to capture the essence of what you were asking. Thanks for your patience.

Dear Chet,
The equations provided by you fully sums up the idea
So the dilemma I have is which one of these approaches is correct?

The first approach is correct, and the second approach is not correct.

Is there a reason I can't substitute both side forces by one?

I don't quite know how to explain to you why the second approach is incorrect. It all depends on what motivated you to think that it could be correct. I personally would not have expected it to be correct. So what was your rationale?

Chet