- #1
fashara
- 4
- 0
Hi, I would like some guidance about a piping problem I have.
I would like to know how to solve this shear stress equation for a narrowing pipe. This equation gives the shear stress on the edges of a cylindrical piece of fluid having radius r and length L within the pipe. I would like to know the total shear stress for the entire pipe. I know that L will be equal to the length of the pipe but the problem is the radius is changing as one moves from left to right down the pipe. The narrowing of the pipe is smooth and hyperbolic in shape. Here is a picture...
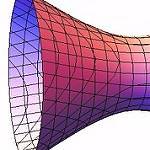 hyperboloid-surface by lkjlkj lkjlkjl, on Flickr
hyperboloid-surface by lkjlkj lkjlkjl, on Flickr
The pipe ends are two circles, circle_1 being on the left and circle_2 being on the right, each having a radius of r_1 and r_2, respectively. (I know the picture isn't exactly right, just pretend there are perfect circles on the left and right hand sides) The fluid flows from left to right and r is decreasing from r_1 to r_2 in the direction of the fluid flow.
* Note r_1 > r_2
Intuitively, I would like to integrate the shear stress equation from r_1 to r_2 but I am not sure if this approach is valid.
The equation for the shear stress is given below:
τ=(r/2)[(-dp)/(dz)]
with r = radius of the pipe
and [(-dp)/(dz)] = change in pressure over change in distance
If I integrate in the way that I mention earlier I get:
τ = -(r^2)/4 (dp/dz)
Is this a correct approach to solving for the shear stress along the pipe?
Thanks!
I would like to know how to solve this shear stress equation for a narrowing pipe. This equation gives the shear stress on the edges of a cylindrical piece of fluid having radius r and length L within the pipe. I would like to know the total shear stress for the entire pipe. I know that L will be equal to the length of the pipe but the problem is the radius is changing as one moves from left to right down the pipe. The narrowing of the pipe is smooth and hyperbolic in shape. Here is a picture...
The pipe ends are two circles, circle_1 being on the left and circle_2 being on the right, each having a radius of r_1 and r_2, respectively. (I know the picture isn't exactly right, just pretend there are perfect circles on the left and right hand sides) The fluid flows from left to right and r is decreasing from r_1 to r_2 in the direction of the fluid flow.
* Note r_1 > r_2
Intuitively, I would like to integrate the shear stress equation from r_1 to r_2 but I am not sure if this approach is valid.
The equation for the shear stress is given below:
τ=(r/2)[(-dp)/(dz)]
with r = radius of the pipe
and [(-dp)/(dz)] = change in pressure over change in distance
If I integrate in the way that I mention earlier I get:
τ = -(r^2)/4 (dp/dz)
Is this a correct approach to solving for the shear stress along the pipe?
Thanks!