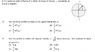Shell and Liquid Forces: Exploring Equilibrium in a Hemispherical Container

[Vibhor]

Homework Statement

Homework Equations

The Attempt at a Solution

Considering the upper hemispherical liquid part ,the forces acting on it are , force due to the shell and that due to the bottom liquid .

Doing a force balance , force due to upper hemispherical shell = $\pi R^3ρg - \frac{2}{3}\pi R^3ρg = \frac{1}{3}\pi R^3ρg$ (downwards)

Force due to the liquid on upper hemisphere would be $\frac{1}{3}\pi R^3ρg$ (upwards) gives option A) for Q 13 .

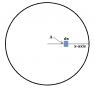
For Q 14 , I think rotating the shell doesn't rotate the liquid which means the pressure at point P should remain unaffected i.e option A )

Is that correct ?

Thanks

 

[TSny]

I guess we assume that the pressure is zero at the point of the liquid at the top of the shell.

I agree with your answer for 13.

I agree with your answer for 14 if the liquid doesn't rotate. But that's not very interesting. I suspect that the problem assumes that the liquid rotates with the shell.

 

[Vibhor]

I suspect that the problem assumes that the liquid rotates with the shell.

In that case do you get any of the four options ?

But that's not very interesting

Would the assumption of liquid rotating suitable for an intro physics problem ?

Assuming the liquid rotates , how should I proceed ?

 

[TSny]

I used simple integration. Maybe there's another way. I'll have to think about it. I'm off to bed for now.

 

[haruspex]

I used simple integration. Maybe there's another way. I'll have to think about it. I'm off to bed for now.

A walk sometimes helps. Forces one to look for ways so easy they can be done in the head. I arrived at one of the options. I did use my knowledge that in an open tank of uniformly rotating liquid the surface is parabolic.

 

[Vibhor]

I arrived at one of the options. I did use my knowledge that in an open tank of uniformly rotating liquid the surface is parabolic.

Is it possible for the liquid to have parabolic surface in this problem ( considering that the shell is completely filled ) ?

Could you please share your reasoning .

 

[haruspex]

Is it possible for the liquid to have parabolic surface in this problem ( considering that the shell is completely filled ) ?

Could you please share your reasoning .

In this case, the sphere is full, so no exposed surface. But does it tell us anything about the surfaces of constant pressure within the liquid?

 

[Vibhor]

the surfaces of constant pressure

 

[haruspex]

Umm... are you hinting that you don't know what I mean by a surface of constant pressure, or you cannot figure out how it relates to the parabolic surface of a partly filled vessel?

 

[Vibhor]

Both .

 

[haruspex]

Both .

A surface of constant pressure just means the locus of points within the liquid where the pressure is constant. Like a line on a contour map, or like an equipotential surface. If the vessel is not full, the exposed surface is the surface at (gauge) pressure zero, i.e. ambient pressure.
Given that in a rotating vessel that is not full the exposed surface would be parabolic, can you see how to show that all constant pressure surfaces within it are parabolic? Think about the force balance on a small parcel of liquid, and which way the pressure gradient points.

 

[TSny]

A walk sometimes helps. Forces one to look for ways so easy they can be done in the head.

Yes, indeed!

I arrived at one of the options. I did use my knowledge that in an open tank of uniformly rotating liquid the surface is parabolic.

Very nice. I guess that pushes the integration back to getting the parabolic equipotentials. But if you already know the formula for the parabolic shape, then this is a very clever way to get the answer to the problem.

 

[Vibhor]

Very nice. I guess that pushes the integration back to getting the parabolic equipotentials.

Are you referring to the equation $y = \frac{ω^2r^2}{2g} + constant$ ? Is this the "simple integration" you were referring to in post#4 ?

But if you already know the formula for the parabolic shape, then this is a very clever way to get the answer to the problem.

I don't see any parabolic shapes in the liquid. The shell is completely full of liquid .

Sorry , I am clueless . What is the clever way you are alluding to ?

 

[TSny]

Are you referring to the equation $y = \frac{ω^2r^2}{2g} + constant$ ? Is this the "simple integration" you were referring to in post#4 ?

I was thinking of starting from scratch. Take a small element of the rotating fluid as shown below. It has a width dx and the areas of the vertical faces perpendicular to the x-axis are A. Apply F = ma in the x direction to find the change in pressure as you move a distance dx along the x-axis.

I don't see any parabolic shapes in the liquid. The shell is completely full of liquid .

Sorry , I am clueless . What is the clever way you are alluding to ?

haruspex's method is clever. But it presupposes that you are already familiar with a well-known result about rotating fluids.

 

[Vibhor]

I was thinking of starting from scratch. Take a small element of the rotating fluid as shown below. It has a width dx and the areas of the vertical faces perpendicular to the x-axis are A. Apply F = ma in the x direction to find the change in pressure as you move a distance dx along the x-axis.

$dP = ρω^2x dx$

$P(x) = \frac{1}{2}ρ ω^2 R^2 + P_{center}$

$P_{center} = ρgR$

$P(x) = \frac{1}{2}ρ ω^2 R^2 + ρgR$

$Pressure(P) = \frac{3}{2}ρgR$ i.e option C)

Is this what you are suggesting ?

 

[haruspex]

$dP = ρω^2x dx$

$P(x) = \frac{1}{2}ρ ω^2 R^2 + P_{center}$

$P_{center} = ρgR$

$P(x) = \frac{1}{2}ρ ω^2 R^2 + ρgR$

$Pressure(P) = \frac{3}{2}ρgR$ i.e option C)

Is this what you are suggesting ?

Very good.

 

[Vibhor]

Thanks .

Just want to clear few things . The sphere is rotating about an axis coming out of the plane of the page . Right ?

 

[haruspex]

Thanks .

Just want to clear few things . The sphere is rotating about an axis coming out of the plane of the page . Right ?

No, it says about the axis z1-z2, which makes it vertical in the diagram. With a horizontal axis, your P_center=ρgR would be doubtful.

 

[Vibhor]

No, it says about the axis z1-z2, which makes it vertical in the diagram.

In that case the pressure at the topmost point of the shell on z1-z2 axis would be 0 and that at the bottommost point would be $2ρgR$ ??

Don't you think the dotted lines at the top and bottom of the shell in the figure indicate that Z1-Z2 axis is coming out of the plane of the page ?

 

[Vibhor]

With a horizontal axis, your P_center=ρgR would be doubtful.

Why ? Is it because pressure "ρgh" holds under hydrostatic conditions which would no longer be the case ?

 

[Vibhor]

Suppose the fluid rotates about an axis coming out of the plane of the figure , then pressure at the topmostpoint (on y-axis ) is $\frac{1}{2}ρgR$ and bottommostpoint (on y-axis ) is $\frac{5}{2}ρgR$ ??

 

[haruspex]

Suppose the fluid rotates about an axis coming out of the plane of the figure , then pressure at the topmostpoint (on y-axis ) is $\frac{1}{2}ρgR$ and bottommostpoint (on y-axis ) is $\frac{5}{2}ρgR$ ??

How do you arrive at that?

 

[haruspex]

Why ? Is it because pressure "ρgh" holds under hydrostatic conditions which would no longer be the case ?

Yes.

 

[haruspex]

that case the pressure at the topmost point of the shell on z1-z2 axis would be 0 and that at the bottommost point would be 2ρgR ??

Yes.

Don't you think the dotted lines at the top and bottom of the shell in the figure indicate that Z1-Z2 axis is coming out of the plane of the page ?

No, why do you think that? Is there some diagrammatic convention regarding dotted lines that I am unaware of?

 

[Vibhor]

How do you arrive at that?

By adding the pressure ( similar to as derived in post #15) to the respective hydrostatic pressures at the two points .

 

[haruspex]

By adding the pressure ( similar to as derived in post #15) to the respective hydrostatic pressures at the two points .

But you seem to have assumed the pressure at the centre is ρgR, which, as I wrote, is not justified.
Think first about the pressure at the top. What does the force balance tell you about that?

 

[Vibhor]

Ok . Thanks TSny and haruspex .

 

[haruspex]

Ok . Thanks TSny and haruspex .

Ok.

The horizontal axis case for an arbitrary rotation rate is quite interesting.

 

[Vibhor]

Please have a look at a previous problem discussed at PF https://www.physicsforums.com/threads/spherical-shell-with-fluid.793060/ .

In this case it was assumed that the fluid doesn't rotate with the shell . How am I suppose to know/assume whether the fluid inside a closed rotating object rotates or not while solving numerical problems ??

 

[TSny]

In that thread it states that the fluid is frictionless, so the liquid can't get any torque from the wall of the shell to start rotating. For this thread, if the liquid did not rotate with the shell, then as you pointed out, the rotation of the shell would not have any effect on the pressure inside the liquid.

 

[Vibhor]

Ok . Thanks .

 

[TSny]

The horizontal axis case for an arbitrary rotation rate is quite interesting.

I'm stumped on one aspect of this case. In order to know the pressure throughout, I first need to know the pressure at one point. In the rotation about a vertical axis we just assumed the pressure is zero at the top.

What if the pressure is zero at the top before any rotation, and then we start rotating about a horizontal axis? Is there a simple way to see what the pressure will be at some one point so I can determine the pressure everywhere else?

 

[haruspex]

I'm stumped on one aspect of this case. In order to know the pressure throughout, I first need to know the pressure at one point. In the rotation about a vertical axis we just assumed the pressure is zero at the top.

What if the pressure is zero at the top before any rotation, and then we start rotating about a horizontal axis? Is there a simple way to see what the pressure will be at some one point so I can determine the pressure everywhere else?

Yes, that's what makes it tricky.
I believe one is justified in saying that the minimum pressure is always zero. Below a threshold rotation that will always be at the top. In the limit it is at the centre.

 

[TSny]

Yes, that's what makes it tricky.
I believe one is justified in saying that the minimum pressure is always zero. Below a threshold rotation that will always be at the top. In the limit is at at the centre.

OK. That makes sense to me. Then I think the threshold is for ω = √(g/R). For larger ω the point of zero pressure will be located a distance r above the center of the sphere where ω²r = g. Is that what you find?

 

[haruspex]

OK. That makes sense to me. Then I think the threshold is for ω = √(g/R). For larger ω the point of zero pressure will be located a distance r above the center of the sphere where ω²r = g. Is that what you find?

Yes.