alane1994
- 36
- 0
I have been going over previous tests in an attempt to better prepare myself for the final that is coming tomorrow. I was posed a question.
Use the shell method to find the volume of the solid generated by revolving the plane region about the given line.
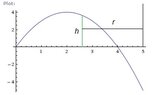
$$y = 4x - x^2$$ , y = 0, about the line x = 5
I know this.
SHELL METHOD
$$V = \int_{a}^{b} 2\pi x (f(x) - g(x))dx$$
I know this is fairly rudimentary, but assistance would be appreciated!
Use the shell method to find the volume of the solid generated by revolving the plane region about the given line.
$$y = 4x - x^2$$ , y = 0, about the line x = 5
I know this.
SHELL METHOD
$$V = \int_{a}^{b} 2\pi x (f(x) - g(x))dx$$
I know this is fairly rudimentary, but assistance would be appreciated!