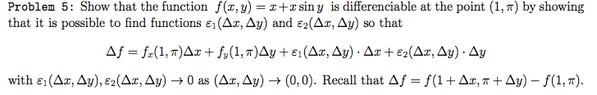Show that f(x,y) is differentiable

[Jamie2]

Problem:
View attachment 2105

I plugged in f_x, f_y, and f(1,pi) everywhere I could but I have no idea how to move on from here. I'm stuck trying to show that:

(1+Δx) + (1+Δx)sin(pi+Δy) - 1 = Δx - Δy + ε(Δx,Δy)Δx + ε(Δx,Δy)Δy

 

[Opalg]

I'm stuck trying to show that:

(1+Δx) + (1+Δx)sin(pi+Δy) - 1 = Δx - Δy + ε(Δx,Δy)Δx + ε(Δx,Δy)Δy

You are nearly there! You want to show that $$(1+\Delta x) + (1+\Delta x)\sin(\pi+\Delta y) - 1 = \Delta x - \Delta y + \varepsilon_1(\Delta x,\Delta y)\Delta x + \varepsilon_2(\Delta x,\Delta x y)\Delta y.$$ On the left side of that equation, $ \sin(\pi+\Delta y) = - \sin(\Delta y)$. So the left side of the equation becomes $$\Delta x - \sin(\Delta y) - \Delta x\sin(\Delta y).$$ You want that to look like the right side of the equation. So write it as $$\Delta x - \Delta y + \Delta x(-\sin(\Delta y) + \Delta y\left(1 - \frac{\sin(\Delta y)}{\Delta y}\right).$$ Now can you see how to choose the functions $\varepsilon_1(\Delta x,\Delta y)$ and $\varepsilon_2(\Delta x,\Delta y)$? (Remember that you have to show that they go to $0$ as $(\Delta x,\Delta y) \to (0,0).$)

 

[Jamie2]

You are nearly there! You want to show that $$(1+\Delta x) + (1+\Delta x)\sin(\pi+\Delta y) - 1 = \Delta x - \Delta y + \varepsilon_1(\Delta x,\Delta y)\Delta x + \varepsilon_2(\Delta x,\Delta x y)\Delta y.$$ On the left side of that equation, $ \sin(\pi+\Delta y) = - \sin(\Delta y)$. So the left side of the equation becomes $$\Delta x - \sin(\Delta y) - \Delta x\sin(\Delta y).$$ You want that to look like the right side of the equation. So write it as $$\Delta x - \Delta y + \Delta x(-\sin(\Delta y) + \Delta y\left(1 - \frac{\sin(\Delta y)}{\Delta y}\right).$$ Now can you see how to choose the functions $\varepsilon_1(\Delta x,\Delta y)$ and $\varepsilon_2(\Delta x,\Delta y)$? (Remember that you have to show that they go to $0$ as $(\Delta x,\Delta y) \to (0,0).$)

thank you! I understand how to finish the problem now. But could you explain your simplification of the left side in a little more detail?