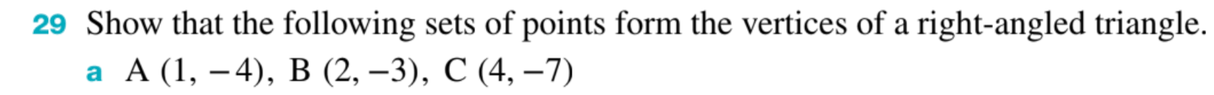Yazan975
- 30
- 0
View attachment 8415
I was thinking of using Pythagoras here but it didn't get me far
Any suggestions?
I was thinking of using Pythagoras here but it didn't get me far
Any suggestions?