- #1
rnielsen25
- 25
- 1
- Homework Statement
- c)
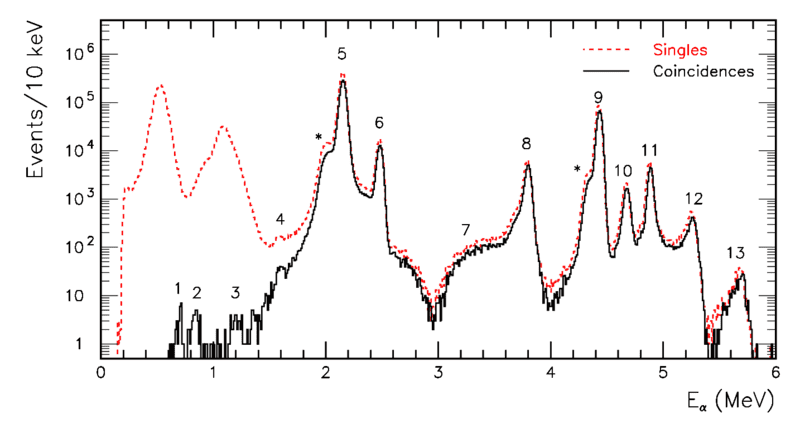
The experimental spectrum of ##{}^{20}Na## can be found below. Apart from peaks that may be fitted with Breit-Wigner type expression like in equation (20.77) there is an interesting minimum close to ##3 \mathrm{MeV}## alpha particle energy. One possible interpretation is that it is due to interference between the strong peak (named 5) just below ##2.2 \mathrm{MeV}## and a quite broad level (named 7) somewhat above ##3 \mathrm{MeV}##. Can you devise an expression that could describe this? [Hint: the rewriting in terms of amplitudes in equation (20.76) will be a better starting point..]
- Relevant Equations
- $$\sigma_r^{b a}=\frac{\pi}{k_a^2}\left|\frac{A^b A^{a *}}{E-E_r+(i / 2) \Gamma_r}\right|^2$$
This problem set considers (beta-delayed) alpha decay of ##{}^{20}Na##. I'm currently stuck in the following exercise and was hoping some of you could help me in the right way. Thanks in advance!
The problem is:
c)
The experimental spectrum of ##{}^{20}Na## can be found below. Apart from peaks that may be fitted with Breit-Wigner type expression like in equation (20.77) there is an interesting minimum close to ##3 \mathrm{MeV}## alpha particle energy. One possible interpretation is that it is due to interference between the strong peak (named 5) just below ##2.2 \mathrm{MeV}## and a quite broad level (named 7) somewhat above ##3 \mathrm{MeV}##. Can you devise an expression that could describe this? [Hint: the rewriting in terms of amplitudes in equation (20.76) will be a better starting point..]
Equation 20.76 is a version of the Breit-Wigner formula given by: $$\sigma_r^{b a}=\frac{\pi}{k_a^2}\left|\frac{A^b A^{a *}}{E-E_r+(i / 2) \Gamma_r}\right|^2$$
Where r refers to a specific resonance. In the case of an isolated resonance, the Breit - Wigner approximation for the reaction cross section ##a \rightarrow b## contains the entrance, ##A^a##, and exit, ##A^b##, amplitudes and the typical resonance denominator that corresponds to the pole ##\mathcal{E}=E_r-(i / 2) \Gamma_r## in the lower part of the complex energy plane.
However, even though I have been given a hint, I'm quite unsure how to approach this problem. I guess I don't really know what it is, I want to show (What expression the hint wants me to find).
My approach would be that a sum of the two resonance cross-sections should describe these two peaks and hence the observed minimum. i.e.
$$\sigma=\sigma_5^{b a} + \sigma_7^{c d} = \frac{\pi}{k_a^2}\left|\frac{A^b A^{a *}}{E-E_5+(i / 2) \Gamma_5}\right|^2 + \frac{\pi}{k_c^2}\left|\frac{A^d A^{c *}}{E-E_7+(i / 2) \Gamma_7}\right|^2$$
Is this correct? But what does the hint really refer to, when it says I should rewrite the expression in terms of amplitudes? Should I attempt to isolate ##|A^b A^{a *}|^2##
The problem is:
c)
The experimental spectrum of ##{}^{20}Na## can be found below. Apart from peaks that may be fitted with Breit-Wigner type expression like in equation (20.77) there is an interesting minimum close to ##3 \mathrm{MeV}## alpha particle energy. One possible interpretation is that it is due to interference between the strong peak (named 5) just below ##2.2 \mathrm{MeV}## and a quite broad level (named 7) somewhat above ##3 \mathrm{MeV}##. Can you devise an expression that could describe this? [Hint: the rewriting in terms of amplitudes in equation (20.76) will be a better starting point..]
Where r refers to a specific resonance. In the case of an isolated resonance, the Breit - Wigner approximation for the reaction cross section ##a \rightarrow b## contains the entrance, ##A^a##, and exit, ##A^b##, amplitudes and the typical resonance denominator that corresponds to the pole ##\mathcal{E}=E_r-(i / 2) \Gamma_r## in the lower part of the complex energy plane.
However, even though I have been given a hint, I'm quite unsure how to approach this problem. I guess I don't really know what it is, I want to show (What expression the hint wants me to find).
My approach would be that a sum of the two resonance cross-sections should describe these two peaks and hence the observed minimum. i.e.
$$\sigma=\sigma_5^{b a} + \sigma_7^{c d} = \frac{\pi}{k_a^2}\left|\frac{A^b A^{a *}}{E-E_5+(i / 2) \Gamma_5}\right|^2 + \frac{\pi}{k_c^2}\left|\frac{A^d A^{c *}}{E-E_7+(i / 2) \Gamma_7}\right|^2$$
Is this correct? But what does the hint really refer to, when it says I should rewrite the expression in terms of amplitudes? Should I attempt to isolate ##|A^b A^{a *}|^2##
