Show that two real distinct roots in the given quadratic equation exist

[chwala]

Homework Statement

See attached

Relevant Equations

discriminants

Find the question below;

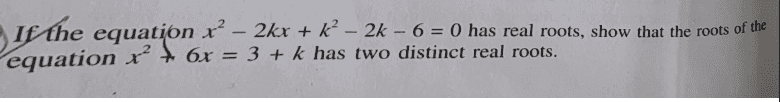
Find my working below;

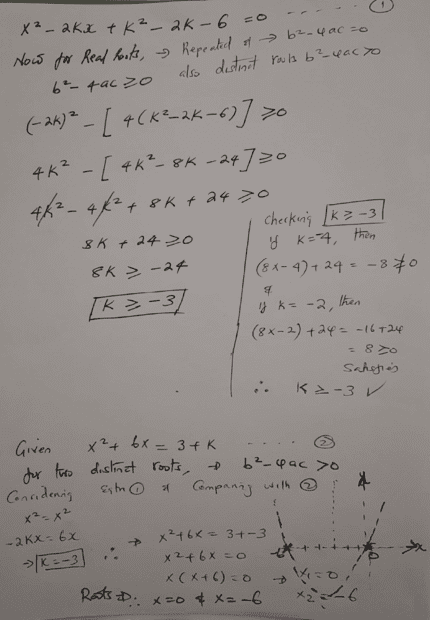
I hope i understood what the question was asking...you may confirm. Cheers guys

 

[PeroK]

I suggest you need to consider $k \ge -3$ not just $k = -3$. In any case, you could do the same analysis for the second equation and get a condition on $k$ for the equation to have distinct real roots. And compare that with $k \ge -3$.

 

[chwala]

Perok, i do not seem to get it...analysing the equation, $x^2+6x= 3+k$, yields $k>-12$, for us to realize two distinct real roots. How am i to relate this with $k≥-3?$
I thought by being given, a condition for coefficient of $x$, in the second equation i.e $x^2+6x=...$, then we were supposed to look for its $k$ value, like i had done...am lost on this...what exactly are we trying to establish? Thanks...

 

[PeroK]

Perok, i do not seem to get it...analysing the equation, $x^2+6x= 3+k$, yields $k>-12$, for us to realize two distinct real roots. How am i to relate this with $k≥-3?$
I thought by being given, a condition for coefficient of $x$, in the second equation i.e $x^2+6x=...$, then we were supposed to look for its $k$ value, like i had done...am lost on this...what exactly are we trying to establish? Thanks...

$k \ge -3 \ \Rightarrow \ k > -12$

 

[chwala]

$k \ge -3 \ \Rightarrow \ k > -12$

Ok, cheers ...noted with regards.

 

[kumusta]

This is how I look at the solution of the problem.
First, by replacing the $~k^2-2k-6~$ by $~r~$ in the first given quadratic equation with real roots and then solving for $~x~$ in terms of $~k~$ and $~k~$, one gets the condition $~k~\geq \pm\sqrt {r}$ for the roots of $~x~$ to be real.
Second, by solving the quadratic equation for $~k~$ in terms of $~r~$ and getting rid of the square root with $~r~$ inside, one gets $~k\geq – 3$ if the condition for the roots of $~x~$ to be real, obtained earlier, is similarly imposed on the roots of $~k~$.
Third, by solving for the second given quadratic equation for $~x~$ in terms of $~k~$ and requiring its roots to be real, too one gets a second condition for $~k~$, namely $~k~\geq– 12$. PeroK got both $~k\geq – 3$ and $~k~\geq– 12$ earlier.
The $~k~\geq– 12$ applied to the second quadratic equation for $~x~$ yields two equivalent real roots, $(x+3)^2 \geq 0$.
The $~k\geq – 3$, however, leads to two distinct roots since one obtains
${~~~~~}k=x^2 + 6x - 3~\geq – 3~\Rightarrow~x(x+6)~\geq~0$

 

[epenguin]

This may be not so very different from what others have said, but you judge.
The way the OP did it was formulaic, relying on the the quadratic solution formula or the discriminant formula. Which is how I would have done it at school and many years after. but whether I remembered where the formula came from, I doubt. It is not that self-evident. Somehow just the formula is the one thing we all remember from school algebra, it is so dinned into us. Often useful, so I suppose worthwhile. on the other hand if math is about remembering formula... I propose the following set out which recalls the 'completing the square' idea which is behind the quadratic solution.

How to complete the square starting $(x^2 - 2kx ...$? Fairly obvious, soon giving us that the first equation can be written
$(x-k)^2 = 2(k+3)$
We see that real roots require $(k+3)≥0$ with equal roots when $≥$ is = .

And completing the square in the second given expression starting $(x^2+6x ... )$? We get
$(x^2+6x+9)=9+(3+k)$
$(x+3)^2=9 +(3+k)$

For this to have real roots, the expression on the right must be positive. But if $(3+k)≥0$ as established in the first part of the argument, then certainly it is, so that the equation has real roots.

Some Profs might prefer this way of setting out the argument. So some smart students might do it that way. Maybe some supersmart students might work it out your way, and then rewrite it my way, which of course is saying exactly the same things but is more explicit.