member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,
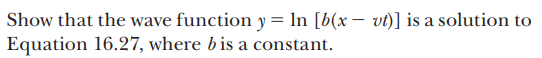
Where equation 16.27 is the wave equation.
The solution is
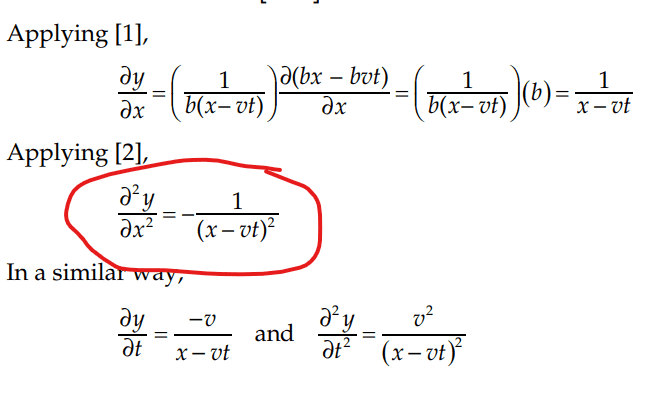

I don't understand how they got the second partial derivative of ##y## with respect to
##x## circled in red.
I thought it would be ##1## since ##v## and ##t## are constants
Many thanks!
Where equation 16.27 is the wave equation.
The solution is
I don't understand how they got the second partial derivative of ##y## with respect to
##x## circled in red.
I thought it would be ##1## since ##v## and ##t## are constants
Many thanks!