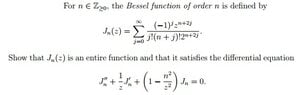- #1
nacho-man
- 171
- 0
Hi,
I actually posted this problem a while back on a separate forums:
Showing the bessel function is entire
And got a response, but still cannot seem to figure out how to do this question
Given a ratio test can be used, we must first define a p(z) and q(z)
so we can see if the sum for $$ \frac{p(z)}{q(z)} $$ converges,
but the denominator doesn't even have a complex variable in terms of $z$, so how is this possible?
Any help is much appreciated, this one is wrinkling my brain!
for z = 0 it converges.
for z =/ 0, we convert it to the form
$\frac{a_n+1}{a_n}$ , or do we use j?
thanks!
I actually posted this problem a while back on a separate forums:
Showing the bessel function is entire
And got a response, but still cannot seem to figure out how to do this question
Given a ratio test can be used, we must first define a p(z) and q(z)
so we can see if the sum for $$ \frac{p(z)}{q(z)} $$ converges,
but the denominator doesn't even have a complex variable in terms of $z$, so how is this possible?
Any help is much appreciated, this one is wrinkling my brain!
for z = 0 it converges.
for z =/ 0, we convert it to the form
$\frac{a_n+1}{a_n}$ , or do we use j?
thanks!
Attachments
Last edited: