zenterix
- 774
- 84
- TL;DR Summary
- I am following the book "Physical Chemistry" by Silbey, Alberty, and Bawendy.
I am having a difficult time with sign conventions used when calculating work done on a closed system containing a gas.
Here is the reasoning as it appears in the book.
Consider the following setup
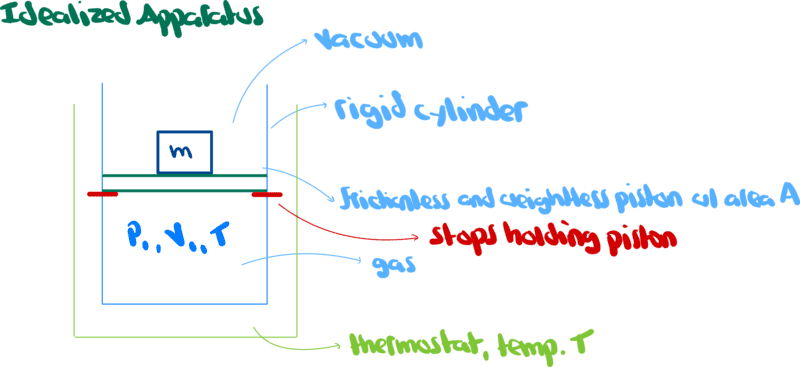
Work (w) is a scalar quantity defined ##w=\vec{f}\cdot\vec{L}##.
where ##\vec{f}## is the vector force and ##\vec{L}## is the vector length of path.
If the force vector of magnitude ##\lVert \vec{f}\rVert## and the vector length of magnitude ##\lVert \vec{L} \rVert## are separated by an angle ##\theta##, the work is given by ##\lVert\vec{f}\rVert\lVert\vec{L}\rVert\cos{\theta}##.
Pressure, ##P## is force per unit area, ie ##P=\frac{\lVert \vec{f}\rVert} {\lVert\vec{A}\rVert}##.
Consider a situation where the gas in the cylinder above is expanding, pushing the piston upward.
The differential quantity of work done by the expanding gas to move the piston a distance ##dL## is, according to the book
$$w=\lVert P\vec{A}\rVert dL=PdV\tag{1}$$
My first question is the following: in the context of (1), it seems that there is an implicit cosine term; that is, (1) is obtained from a dot product, and hence it seems that ##\lVert P\vec{A}\rVert## and ##dL## must all be positive, and that implicitly we have a ##\cos{0}=1## term. Is this correct?
If it is correct, then ##dV## can also only be positive in (1).
On the other hand, we could write out
$$w=\lVert P\vec{A}\rVert dL\cos{\theta}=PdV\tag{2}$$
where ##dV## is now ##\lVert \vec{A}\rVert dL\cos{\theta}##, in which case ##dV## can be negative.
The book then says
This is a bit confusing to me. As far as I know, work is done by a force. Whether the gas expands and pushes the piston up, or the gas is compressed as the piston moves down, we have a pair of Newton's third law forces shared between the piston and the mass, and between the piston and the gas.
Each force does some amount of work.
The book has this depiction
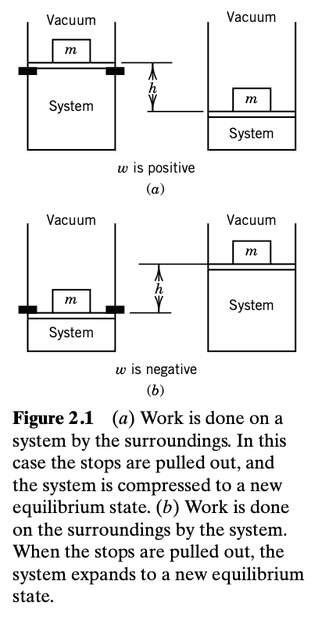
As far as I can tell,
in (a), the force applied by the piston on the gas (which is the same as the force applied by the mass onto the piston, since the latter has zero mass and there is no friction with the cylinder) is in the same direction as the displacement vector of the gas. This is the same work done by the force of the mass on the piston and is positive.
in (b), the force applied by the piston on the gas is in the opposite direction to the displacement of the gas, and so the work done by this force is negative.
Now, the convention says that in (a) work is "done on the system" and in (b) work is "done on the surroundings", and also that $$dw=-P_{ext}dV$$.
##P_{ext}## is said to be the external pressure, that is, the pressure of the piston on the gas.
Putting everything together, it seems that in (a) what is happening is that the force created by the mass on top of the piston is doing positive work and in (b) it is doing negative work. These results come out from the expression
$$\lVert P\vec{A}\rVert dL \cos{\theta}$$
However, the book uses another expression
$$-P_{ext}dV$$
Now, ##P## is the same as ##P_{ext}##. It is not clear to me how to reconcile these two expressions as it concerns the ##dV## term. It would seem that it is as simple as
$$dV=-\lVert \vec{A} \rVert dL\cos{\theta}$$
In my opinion, all the confusion arising from all of this is because the book in question isn't great.
Consider the following setup
Work (w) is a scalar quantity defined ##w=\vec{f}\cdot\vec{L}##.
where ##\vec{f}## is the vector force and ##\vec{L}## is the vector length of path.
If the force vector of magnitude ##\lVert \vec{f}\rVert## and the vector length of magnitude ##\lVert \vec{L} \rVert## are separated by an angle ##\theta##, the work is given by ##\lVert\vec{f}\rVert\lVert\vec{L}\rVert\cos{\theta}##.
Pressure, ##P## is force per unit area, ie ##P=\frac{\lVert \vec{f}\rVert} {\lVert\vec{A}\rVert}##.
Consider a situation where the gas in the cylinder above is expanding, pushing the piston upward.
The differential quantity of work done by the expanding gas to move the piston a distance ##dL## is, according to the book
$$w=\lVert P\vec{A}\rVert dL=PdV\tag{1}$$
My first question is the following: in the context of (1), it seems that there is an implicit cosine term; that is, (1) is obtained from a dot product, and hence it seems that ##\lVert P\vec{A}\rVert## and ##dL## must all be positive, and that implicitly we have a ##\cos{0}=1## term. Is this correct?
If it is correct, then ##dV## can also only be positive in (1).
On the other hand, we could write out
$$w=\lVert P\vec{A}\rVert dL\cos{\theta}=PdV\tag{2}$$
where ##dV## is now ##\lVert \vec{A}\rVert dL\cos{\theta}##, in which case ##dV## can be negative.
The book then says
Work ##w## can be positive or negative since work may be done on a system or a system may do work on its surroundings. The convention on ##w## is that it is positive when work is done on the system of interest and negative when the system does work on the surroundings. Thus, the differential of the ##PV## work don on a system is given by $$dw=-P_{ext}dV$$ where ##P_{ext}## is the external or applied pressure.
This is a bit confusing to me. As far as I know, work is done by a force. Whether the gas expands and pushes the piston up, or the gas is compressed as the piston moves down, we have a pair of Newton's third law forces shared between the piston and the mass, and between the piston and the gas.
Each force does some amount of work.
The book has this depiction
As far as I can tell,
in (a), the force applied by the piston on the gas (which is the same as the force applied by the mass onto the piston, since the latter has zero mass and there is no friction with the cylinder) is in the same direction as the displacement vector of the gas. This is the same work done by the force of the mass on the piston and is positive.
in (b), the force applied by the piston on the gas is in the opposite direction to the displacement of the gas, and so the work done by this force is negative.
Now, the convention says that in (a) work is "done on the system" and in (b) work is "done on the surroundings", and also that $$dw=-P_{ext}dV$$.
##P_{ext}## is said to be the external pressure, that is, the pressure of the piston on the gas.
Putting everything together, it seems that in (a) what is happening is that the force created by the mass on top of the piston is doing positive work and in (b) it is doing negative work. These results come out from the expression
$$\lVert P\vec{A}\rVert dL \cos{\theta}$$
However, the book uses another expression
$$-P_{ext}dV$$
Now, ##P## is the same as ##P_{ext}##. It is not clear to me how to reconcile these two expressions as it concerns the ##dV## term. It would seem that it is as simple as
$$dV=-\lVert \vec{A} \rVert dL\cos{\theta}$$
In my opinion, all the confusion arising from all of this is because the book in question isn't great.
Last edited: