B Sign conventions in torque and non-uniform circular motion

[DrBanana]

Sorry for the overly general title but my problem is regarding a specific problem: find the net force on the bob of a pendulum as a function of $\theta$, the angle it makes with the vertical (assuming the observer is stationary with respect to point from which the string is hung and the vertical beam of the pendulum).

The easy way: If the maximum angular displacement is $\theta_0$, then the tension for a general angle $\theta$ will be $T=mg(3\cos\theta-2\cos\theta_0)$. This force points along the string, so we know its direction. The only other force is the weight. To solve the problem, we just take the resultant of these two forces.

The hard way: I'll abbreviate a 'Leap of faith' as LOF. The bob undergoes non-uniform circular motion (behold my epic drawing skills).

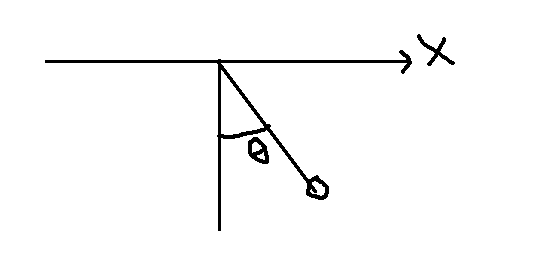It's position can be described with a vector $r$ such that $r=|r|(\sin\theta \hat{i}-\cos\theta \hat{j})$. By definition, velocity is the derivative of the position: $v=|r|\theta'(t)(\cos\theta \hat{i} +\sin\theta \hat{j})$. This is where I first run into problems. If I were measuring $\theta$ with its starting position on the positive x axis, I could just define $\omega$ (the angular speed) as the derivative of $\theta$ with respect to time. However, can I do that here? I must make a choice, and the particular choice I make here is that I let the displacement of the bob along the circular arc (starting from the x axis) take negative values for clockwise directions, so that the displacement $s=|r|(\theta-\frac{\pi}{2})$. Then we can see that $\omega=\frac{d\theta}{dt}$ (LOF number 1). If we differentiate the velocity vector again, we get $a=-\omega^2r+ \alpha (\cos\theta \hat{i} + \sin\theta \hat{j})$, where $a$ is the acceleration vector and $\alpha$ is the angular acceleration, which, by definition, is the derivative of the angular speed. It just so happens that $\theta '' (t) = \alpha$.

We know that $\tau=I\alpha$, where $\tau$ is torque, $I$ is the moment of inertia and alpha is the angular acceleration. LOF number two: the angular acceleration formulated in the previous paragraph, is the same as this angular acceleration.

We also know that $\tau = -mg|r|\sin\theta$. Then $I\alpha=mgr \sin\theta$ so $\alpha=-\frac{g}{r}\theta$ for small values of $\theta$. LOF number 3 is, we can actually write this equation. This is perhaps my main point of confusion. For springs I can understand why the restoring force (and thus the acceleration) should have a sign opposite to the displacement, and for pendulums also I can sort of get a feel for why the torque needs to be 'opposite' in sign to the angular displacement, although not fully. For the spring example, the force vector and the displacement vector are in the same plane, so there is a meaning of the word opposite. However torque as a vector extends out from the page, and there is no vector quantity on the right hand side of the equation that does that. I thought that with these mechanics problems you can either write equations of vectors, or of their magnitudes (no directions), but not something in between.

Anyway, assuming I could write that, it would be possible to solve the differential equation and find the $\omega^2$ term (we would need to specify the maximum angular displacement as well) in terms of $\theta$. After that we could plug in any value of theta in the net acceleration equation and find the corresponding force.

Using both methods, I find that the results are approximately equal. Are all of the leaps of faith I took luck, or did those work, and if so, why?

 

[kuruman]

If I were measuring $\theta$ with its starting position on the positive x axis, I could just define $\omega$ (the angular speed) as the derivative of $\theta$ with respect to time. However, can I do that here?

Why not? Let $\phi$ be the angle w.r.t. the positive x-axis increasing clockwise and $\theta$ be as shown in your drawing. Then
$\phi+\theta=\frac{\pi}{2}\implies \dot{\phi}+\dot{\theta}=0.$
This says that one increases at the same rate as the other one decreases.