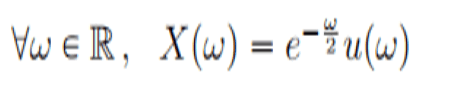You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Engineering Signal & System CTFT: Find x(t) from X(ω)
AI Thread Summary
The discussion revolves around finding the continuous-time signal x(t) from its continuous-time Fourier transform (CTFT) X(ω). Participants express difficulty in determining the limits and seek hints from Fourier transform tables. One user mentions that their approach did not align with the solution provided by their professor, prompting them to seek clarification. The conversation highlights the challenges in applying Fourier transform concepts and the importance of referencing established tables for assistance. Ultimately, the need for collaborative problem-solving in understanding CTFT is emphasized.
Physics news on Phys.org
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
hquang001
- 31
- 3
Oh, my professor never mention this, i will check this and seeBvU said:
Thank you
MathematicalPhysicist
Science Advisor
Gold Member
- 4,662
- 372
##\exp(n(jt-1/2))-1\to -1## as ##n\to \infty## since ##\exp(jtn)=\cos(tn)+j\sin(tn)## and ##\exp(-n/2)\to 0## as ##n\to \infty##.
hquang001
- 31
- 3
Yes i have tried this before, but it didn't match the solution that my professor gave, that's why i ask in here to checkMathematicalPhysicist said:##\exp(n(jt-1/2))-1\to -1## as ##n\to \infty## since ##\exp(jtn)=\cos(tn)+j\sin(tn)## and ##\exp(-n/2)\to 0## as ##n\to \infty##.
My solution: v = 2*t + 5*t^2. dx/dt = 2*t + 5*t^2. Therefore dx = (2t + 5t^2)dt. After taking the anti derivative my equation is s = t^2/2 + 5/3(t^3).
Hello everyone, it's not really for my homework (because I'm not at school anymore) but I'm new and I don't know how to start a new forum. I've never done automatic before and I need help.
I have a 2nd ordre PLL on MATLAB, with an NCO and a PI corrector; the PLL works via the Mid/End algorithm (that's part is ok). I need to find the link between the theoretical formulas and their values in the code to find the value of the gain Ki, and possibly that of Kp if it's not correct. Unfortunately...
Hi all,
I have a structural engineering book from 1979. I am trying to follow it as best as I can. I have come to a formula that calculates the rotations in radians at the rigid joint that requires an iterative procedure. This equation comes in the form of:
$$ x_i = \frac {Q_ih_i + Q_{i+1}h_{i+1}}{4K} + \frac {C}{K}x_{i-1} + \frac {C}{K}x_{i+1} $$
Where:
## Q ## is the horizontal storey shear
## h ## is the storey height
## K = (6G_i + C_i + C_{i+1}) ##
## G = \frac {I_g}{h} ##
## C...
Similar threads
- Replies
- 2
- Views
- 2K
- Replies
- 4
- Views
- 3K
- Replies
- 1
- Views
- 3K
- Replies
- 1
- Views
- 2K
- Replies
- 6
- Views
- 5K
- Replies
- 7
- Views
- 3K
- Replies
- 7
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 2K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Engineering Diff gain of a push pull degenerated differential pair
- Started by arhzz
- Replies: 6
- Engineering and Comp Sci Homework Help
-
Engineering AGMA pitting resistance factor of safety (SH)
- Started by ironfalls18
- Replies: 2
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math