SumDood_
- 39
- 6
- Homework Statement
- Determine the convolution of x(t) and h(t)
- Relevant Equations
- Specified in the solution attempt
So, the convolution of two signals is described as follows:
$$ \int_{-\infty}^{\infty} x(\tau)h(t-\tau) \, d\tau $$
The figure shows the given signals. Now, as described in the convolution integral, I transformed ##h(t)## to ##h(-\tau)## by flipping the signal horizontally. So, now I have an impulse signal when ##\tau = -2##.
Now, the ##t## represents a horizontal shift in signal ##h(t-\tau)##. After which both signals are multiplied and then integrated. When, ##t<1##, then there is no overlap between ##h(\tau)## and ##x(\tau)##. The same is true when ##t>5##.
Now, I need to determine what the limits of the integration would be when there is an overlap between the two signals. If ##h(\tau)## were a rectangular signal, then it would be straightforward.
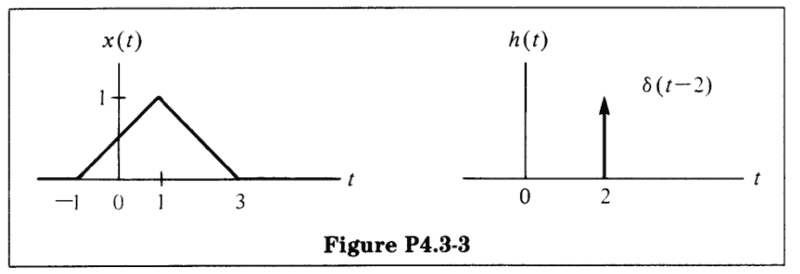
The impulse signal means the only overlap between the two signals exist at the exact point to where the impulse is shifted. Because of this, I don't know how to find the limits to evaluate the convolution integration. From what I have read online, I see that the output signal ##y(t)## is probably a horizontal shifted signal of ##x(t)## by 2 units to the right.
I can't seem to get the answer because I don't know what the limits of the integration are supposed to be. I thought the upper limit and the lower limit would be equal, but then the integration would evaluate to 0.
$$ \int_{-\infty}^{\infty} x(\tau)h(t-\tau) \, d\tau $$
The figure shows the given signals. Now, as described in the convolution integral, I transformed ##h(t)## to ##h(-\tau)## by flipping the signal horizontally. So, now I have an impulse signal when ##\tau = -2##.
Now, the ##t## represents a horizontal shift in signal ##h(t-\tau)##. After which both signals are multiplied and then integrated. When, ##t<1##, then there is no overlap between ##h(\tau)## and ##x(\tau)##. The same is true when ##t>5##.
Now, I need to determine what the limits of the integration would be when there is an overlap between the two signals. If ##h(\tau)## were a rectangular signal, then it would be straightforward.
The impulse signal means the only overlap between the two signals exist at the exact point to where the impulse is shifted. Because of this, I don't know how to find the limits to evaluate the convolution integration. From what I have read online, I see that the output signal ##y(t)## is probably a horizontal shifted signal of ##x(t)## by 2 units to the right.
I can't seem to get the answer because I don't know what the limits of the integration are supposed to be. I thought the upper limit and the lower limit would be equal, but then the integration would evaluate to 0.