Signals & Systems - Stable or Not?

[Angello90]

Homework Statement

The system with impulse response $$h(t) = a_{1}\delta(t-t_{1}) + a_{2}\delta(t-t_{2})$$. Is this system stable or not?

Homework Equations

The Attempt at a Solution

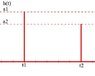
I drew the h(t) response and I got something like that:

but I don't really know how to prove it. There is no input give, only input response.
I would say that it is iff $$-1\leq a_{1} \leq 1$$ & $$-1\leq a_{2} \leq 1$$, since for this values input (if it was a unit step, say) would be bounded, thus producing bounded output. I.E. BIBO stable. Is that right?

Thanks guys!

Homework Statement

Homework Equations

The Attempt at a Solution

 

[marcusl]

Write down the output of this system for an arbitrary input x(t). Is the output bounded if the input is finite?

 

[Angello90]

Ok so I think I have the main idea but one question.
How one may integrate impulse response?
$$\int_{-\infty}^{\infty}\delta(\tau-t)d\tau$$

I know that for step unit, integral would be:
$$\int_{-\infty}^{\infty}u(\tau-t)d\tau = \int_{t}^{\infty}d\tau$$
since step unit is 0 before t.

Would it be true to say that:
$$\int_{-\infty}^{\infty}\delta(\tau-t)d\tau = \int_{0}^{t}d\tau$$

Thanks

 

[marcusl]

No, the integral of a delta function is one so long as the interval includes the point at which its argument is zero. In the case you gave, the delta function is zero except at tau=t, but this is in the interval -inf to +inf so
$$\int_{-\infty}^{\infty}\delta(\tau-t)d\tau =1$$

 

[Angello90]

Thanks mate, I remember that from a lecture except it was
$$\int_{-\infty}^{\infty}\delta(\tau)d\tau =1$$

Anyway thanks! This module is so confusing. Almost too abstract as for engineering course!

 

[Angello90]

I got another problem though.
How should I integrate:
$$\int_{-\infty}^{\infty}e^{-(t-\tau)}sin(t-\tau) d\tau$$

I know I can bring one e to the front:
$$e^{-t}\int_{-\infty}^{\infty}e^{\tau}sin(t-\tau) d\tau$$
but what do I do with sin()? I used trigonometric property on it:
$$sin(A+B) = sin(A)cos(B)-cos(A)sin(B)$$
and got:
$$e^{-t}(sin(t)-cos(t))\int_{-\infty}^{\infty}e^{\tau}(cos(\tau)-sin(\tau)) d\tau$$

Should I expand it into two integrals and use integration by parts? Or am I wasting my time?

 

[marcusl]

Thanks mate, I remember that from a lecture except it was
$$\int_{-\infty}^{\infty}\delta(\tau)d\tau =1$$

Anyway thanks! This module is so confusing. Almost too abstract as for engineering course!

If you are integrating from -inf to +inf, the offset is irrelevant. Change variables u=tau-t and evaluate the integral, to prove it to yourself.

I got another problem though.
How should I integrate:
$$\int_{-\infty}^{\infty}e^{-(t-\tau)}sin(t-\tau) d\tau$$

I know I can bring one e to the front:
$$e^{-t}\int_{-\infty}^{\infty}e^{\tau}sin(t-\tau) d\tau$$
but what do I do with sin()?

I would express sin as a complex exponential. You need to think a little about what the resulting integrals evaluate to.