Signs of the voltage drops in this LC Circuit

[LCSphysicist]

Homework Statement

.

Relevant Equations

.

I have been studying electronical circuit. In general, it is not difficult and is more about to solve EDO. The main problem is, really, the signs.
See as follows:

$$V_{L} = L dI/dt, V_{c} = +- Q/C$$ ?
Should i put a minus sign there? Or shout i maintain the signs? When do i know what sign to use? Even about the voltage dro pacross the inductor, couldn't it be $V = -L dI/dt$?

 

[DaveE]

Homework Statement:: .
Relevant Equations:: .

I have been studying electronical circuit. In general, it is not difficult and is more about to solve EDO. The main problem is, really, the signs.
See as follows:

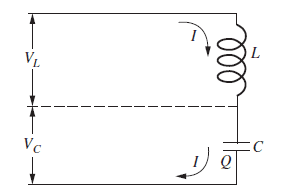
View attachment 286374$$V_{L} = L dI/dt, V_{c} = +- Q/C$$ ?
Should i put a minus sign there? Or shout i maintain the signs? When do i know what sign to use? Even about the voltage dro pacross the inductor, couldn't it be $V = -L dI/dt$?

The signs you apply are quite arbitrary, it doesn't matter how you define voltage and current polarities initially. However. it is ESSENTIAL that you are then consistent when you write out the circuit equations and that you correctly account for the sign conventions that you initially chose.

In your schematic, the current polarity has been documented, but not the voltage polarity, so we can't tell you if $V_{c} = Q/C$ or $V_{c} = - Q/C$, you get to choose that. This is why it's really important when you are communicating your results to others that you include your polarity definitions.

Most all EEs prefer the "passive sign convention" for components. This is where the current polarity flows from the higher potential side of the component to the lower potential side; i.e. V=I*R, not V=-I*R.

Other common conventions are that all currents flow into a node (note, this guarantees that some are negative, which is OK). Also people seem to prefer currents that flow clockwise around loops. However, these last two conventions usually can't be consistently applied to anything but the simplest networks.

Honestly, I think people might be better off just assigning all of these randomly. Then you'll know they could be backwards and you will be more careful about consistency.

Finally, when you solve your circuit equations, some results will may be negative. This is fine, it just means the polarity you initially chose was backwards from reality. That doesn't matter because when ever there is a polarity involved, YOU HAVE TO go back and refer to the definitions.

 

[Delta2]

In DC circuits, once you chose a positive direction for the current then the polarity of the voltages for all elements, R,L,C is that is positive at the end of the component that the current enters into , and is negative at the end of the component where the current exits from. So in your example the top ends of the inductor and the capacitor are positive and the lower ends are negative. However it might turn out that after you done the current calculations that the current is negative, which means that it flows opposite to the positive direction you have initially chosen, so the current directions and polarities will have to be reversed . But that's something you will know after you have done the calculations.

In AC circuits, for resistors the current is in phase with the voltage, which means that similar to DC circuits the polarity is known once you know the direction of current. However for inductors and capacitors the current has a phase difference of $\pi/2$ and $-\pi/2$ respectively with the voltage, which means that the current might be positive while the voltage negative. You need to know the exact moment in time, so you can determine the exact phase , and then to determine whether the current and voltage are positive or negative.

PS. I was partially wrong in the first paragraph, even in DC circuits you might have a current flowing in a component from the negative end of the component to the positive end. This happens when a capacitor or an inductor are discharging, that is when they give their stored electric or magnetic field energy back to the rest of the circuit. Then the current inside the inductor flows from its negative to its positive end, while in the rest of the loop where the inductor is attached to, flows from the positive to the negative end.