Simple Addition of Vector Forces on an Eye-Hook

[sHatDowN]

Homework Statement

Simple Addition

Relevant Equations

Vector

The screw eye is subjected to two forces, F1 and F2. Determine the magnitude and direction of the resultant force.

 

[BvU]

Hi,

The pf guidelines require that you post an attempt at solution ...
Can you find the components of the two forces?

$\$

 

[sHatDowN]

Hello,
I know this way to solve
R²=P²+Q²-2pQ CosB

Then our B is 115 degree
But our Q is unknown

 

[haruspex]

Hello,
I know this way to solve
R²=P²+Q²-2pQ CosB

Then our B is 115 degree
But our Q is unknown

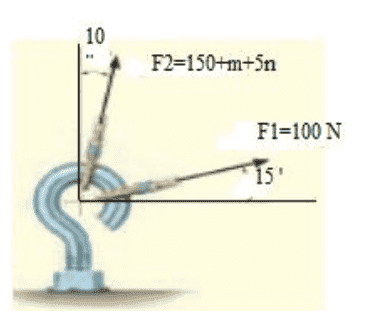
Please state how you are matching up p, q, r to the diagram.

 

[sHatDowN]

And R is resultant

 

[BvU]

Nice, but that does not answer @haruspex 'question ...

 

[kuruman]

How does one interpret the label F2 = 150+m+5n in the drawing?

 

[haruspex]

View attachment 322805
And R is resultant

Have you quoted the whole question? Is there no explanation of what m and n are?

 

[sHatDowN]

m=12
n=5
I find out answer like that :

R=245N
θ=87.6

 

[jbriggs444]

m=12
n=5
I find out answer like that :

R=245N
θ=87.6

Can you show your work for that? I get a different answer.

Edit: Unlike @haruspex, I get something a bit larger for R and something very different for $\theta$. I am taking theta to be the angle in the first quadrant where the resultant lies.

[Calculated twice. Once with paper and pencil and calculator, a second time writing a program using same algorithm. Same answer both times -- once I remembered to convert to radians and back]

 

[haruspex]

m=12
n=5
I find out answer like that :

R=245N
θ=87.6

I get a slightly smaller answer for R, but how are you defining θ and how are you calculating it?

 

[sHatDowN]

 

[sHatDowN]

actually θ is between P and R
and 65° is between P and Q

 

[haruspex]

View attachment 322826

That last equation appears to be a misremembered version of the sine rule.

The question does not specify what direction to measure the angle from, but it would be unusual to measure it from one of the applied forces. You should measure it the same way the given angles are measured, i.e. from one of the axes.

Edit… and your cos rule equation cannot be what you meant. It's either minus at the end or cos(180-115).

 

[jbriggs444]

actually θ is between P and R
and 65° is between P and Q

Then why are you using 115 instead of 65?!

How did you manage to get a near correct answer out of an incorrect formula? Using 115 degrees instead of 65 should have yielded a result of 170.77

When in doubt about the validity of a formula, try it with some extreme values like 0 degrees, 90 degrees and 180 degrees to see whether it will yield the expected results.

C:\Users\John>eyehook.pl
Computing the resultant for f1 + f2 where
f1 = 100 at an angle of 15
f2 = 187 at an angle of 80
Total x: [elided]
Total y: [elided]
Angle between vectors (0 degrees = parallel): 65
Incorrect angle between vectors (180 degrees = parallel): 115
Cosine formula magnitude: [elided]
Cosine formula magnitude with incorrect angle: 170.772003006634
Magnitude = [elided] [Correct result returned from different formula altogether]
Direction = [elided]

I do not comprehend your calculation for theta at all.

 

[sHatDowN]

I solved exact like this

 

[sHatDowN]

I do not comprehend your calculation for theta at all.

It's Come from sin law

 

[haruspex]

It's Come from sin law

View attachment 322830

In post #12 you wrote $\frac Aa=\frac Bb$, but I assume that was just a typo.
As I indicated, the question setter would be expecting the direction to be specified as measured from one of the axes, like the 10° and 15°are, not from P.

 

[sHatDowN]

In post #12 you wrote $\frac Aa=\frac Bb$, but I assume that was just a typo.
As I indicated, the question setter would be expecting the direction to be specified as measured from one of the axes, like the 10° and 15°are, not from P.

Sorry sir, I did not understand what you are saying

 

[haruspex]

Sorry sir, I did not understand what you are saying

Which bit?
In post #12 you wrote $\frac{115}{245}=\frac\theta {187}$, instead of $\frac{\sin(115)}{245}=\frac{\sin(\theta)} {187}$. I assumed it was a typo, but it seems you actually used the misstated version.

The question setter gave you angles relative to two axes at right angles. Your answer for the direction of the resultant should also be relative to one of those two axes. The way you tried to use the sine rule, had you used it correctly, you would have found the angle between P and R. So you should then have added 15° to get the angle between the axis and R.

 

[sHatDowN]

In post #12 you wrote , instead of . I assumed it was a typo, but it seems you actually used the misstated version.

Yes,sorry sir I was on mistake.
I try again and findout 43.4

 

[jbriggs444]

I solved exact like this
[... converting graphic to $\LaTeX$...]
$$R^2 = P^2 + Q^2 - 2PQ \cos \theta$$

In this formula, $\theta$ is taken to be the angle formed between the head of the one vector and the tail of the other. So that parallel vectors will form an angle of 180 degrees.

The way I would measure the angle between two vectors is tail to tail so that parallel vectors will form an angle of 0 degrees. Accordingly, the formula that I would use would be$$R^2 = P^2 + Q^2 + 2PQ \cos \theta$$
This explains how you were able to obtain an approximately correct magnitude from an apparently incorrect angle. Round-off error explains the discrepancy between your 245 N and a more accurate figure of 247 N.

Now then, on to your calculation for $\theta$. You have given two formulas for $\theta$. The first is the one that you claim to have used:$$\frac{115}{245} = \frac{\theta}{187}$$You are dividing one angle by a length and then equating that to another angle divided by another length. That is not justified.

As a justification for this, you call upon something that you call the "sin rule":$$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$$This law holds for a triangle with sides of length a, b and c and angles opposite these sides equal to A, B and C respectively.

The problem is that the law of sines does not divide an angle by a length. It divides the sine of an angle by a length. If you use the law of sines, you need to use sines. [If you were trying to invoke the small angle approximation, it only works for small angles].

The result that you get from the calculation that you claim to have performed is 87.5 degrees. You claim that this angle is measured (counter-clockwise?) from the angle of force $F_1$. That would put the resulting direction somewhere in the second quadrant.

You cannot add two vectors that are both in the first quadrant and expect a result in the second quadrant.

 

[sHatDowN]

Now then, on to your calculation for . You have given two formulas for . The first is the one that you claim to have used:You are dividing one angle by a length and then equating that to another angle divided by another length. That is not justified.

Yes sir i was on mistake and i tried again and find 43.4 .
is that correct?

 

[jbriggs444]

Yes,sorry sir I was on mistake.
I try again and findout 43.8

43.8 degrees counter-clockwise from the 15 degree angle of $F_1$?

That is close to what I get. Can you confirm what angle you are reporting and calculate it accurately?

C:\Users\John>eyehook.pl
Computing the resultant for f1 + f2 where
f1 = 100 at an angle of 15
f2 = 187 at an angle of 80
Total x: 129.064791852623
Total y: 210.040954323535
Small angle between vectors (0 degrees = parallel): 65
Large angle between vectors (180 degrees = parallel): 115
Cosine formula magnitude (large angle and minus sign): 246.52570452004
Cosine formula magnitude (small angle and plus sign): 246.52570452004
Magnitude from Pythagoras = 246.52570452004
Direction = 58.4303392580617
Direction relative to F1 = 43.4303392580617

Spoiler

#!/usr/bin/perl

use strict;
use Math::Trig;

# Conversion factors
my $degrees = pi/180; # Radians per degree
my $radians = 180/pi; # degrees per radian

# Inputs...
my $m = 12;
my $n = 5;
my $f2 = 150 + $m + 5 * $n;

my $f1 = 100;

my $f2_angle = 80 * $degrees;
my $f1_angle = 15 * $degrees;

print "Computing the resultant for f1 + f2 where\n";
print "f1 = $f1 at an angle of ", $f1_angle * $radians, "\n";
print "f2 = $f2 at an angle of ", $f2_angle * $radians, "\n";

# Intermediates...
my $f1y = $f1 * sin ( $f1_angle );
my $f1x = $f1 * cos ( $f1_angle );

my $f2y = $f2 * sin ( $f2_angle );
my $f2x = $f2 * cos ( $f2_angle );

my $xtot = $f1x + $f2x;
my $ytot = $f1y + $f2y;

print "Total x: $xtot\n";
print "Total y: $ytot\n";

# Alternate magnitude...
my $angle_between_inputs = abs( $f1_angle - $f2_angle );
my $large_angle = 180 * $degrees - $angle_between_inputs;
print "Small angle between vectors (0 degrees = parallel): ", $angle_between_inputs * $radians, "\n";
print "Large angle between vectors (180 degrees = parallel): ", $large_angle * $radians, "\n";

my $alternate_magnitude = sqrt ( $f1 * $f1 + $f2 * $f2 + 2 * $f1 * $f2 * cos ( $angle_between_inputs ) );
my $erroneous_magnitude = sqrt ( $f1 * $f1 + $f2 * $f2 - 2 * $f1 * $f2 * cos ( $large_angle ) );

print "Cosine formula magnitude (large angle and minus sign): $alternate_magnitude\n";
print "Cosine formula magnitude (small angle and plus sign): $erroneous_magnitude\n";

# Finals...
my $magnitude = sqrt( ($xtot * $xtot) + ( $ytot * $ytot ) );
my $direction = atan ( $ytot / $xtot ) * $radians;

# Print
print "Magnitude from Pythagoras = $magnitude\n";
print "Direction = $direction\n"; 
print "Direction relative to F1 = ", $direction - $f1_angle * $radians, "\n";

 

[sHatDowN]

43.8 degrees counter-clockwise from the 15 degree angle of ?

Yes,between P and R.
from x-axis is 58.4

 

[jbriggs444]

Yes,between P and R.
from x-axis is 58.4

You realize that 58.4 minus 15 is 43.4, not 43.8, right?

 

[sHatDowN]

You realize that 58.4 minus 15 is 43.4, not 43.8, right?

yes, I edited