- #1
Tanya Sharma
- 1,540
- 135
Homework Statement
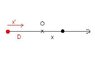
While analyzing superposition of waves from two coherent sources ,the displacement from the two sources are written as y1=A1cos(kx-ωt) and y2=A2cos(kx-ωt+∅) .The resultant displacement at any point is given by y=y1+y2 .
I am having doubt that why does argument of sine in both y1 and y2 contain the same variable ‘x’ . Since ‘x’ represents the distance of the point from the originating source which may be different in the two waves,the displacements should be written as y1=A1cos(kx1-ωt) and y2=A2cos(kx2-ωt+∅) .But this is not the case .
I am pretty sure I am missing something very obvious .I would be grateful if somebody could help me understand this.
Last edited: