Simple lateral vehicle dynamics model

[s_aldworth]

I have run into a problem when trying to model a simplified vehicle that has three degrees of freedom – roll, vertical and lateral motions. It is represented by a single mass with two links that model the suspension behaviour. The links connect the tyre-to-ground contact points (tc) to the body at the ‘roll centres’ (rc). The motion of the points tc and rc are described by known polynomial curves that are a function of the body position relative to ground, so the link lengths and angles to ground vary according to the motion of the body. However, rc is always directly below cg.

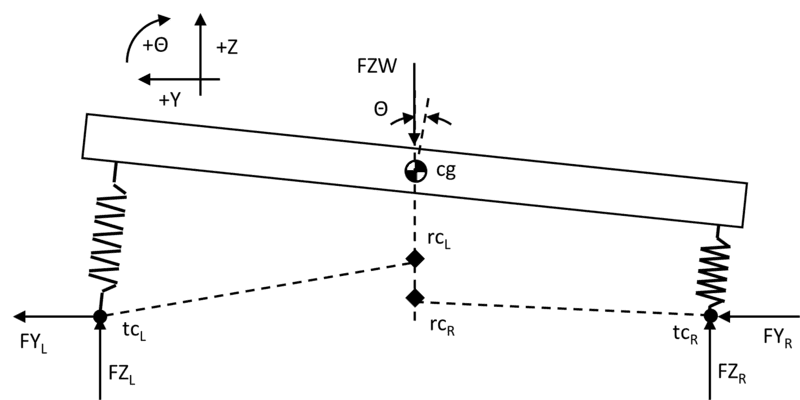
The suspension between the body and the tc points consists of three elements that are described by the body position and velocity relative to ground. Forces are also transmitted to the body through the two links and being massless these are calculated using static force and moment balance equations.

The input to the model is a lateral force (FY) but this force is shared between the two tc points in proportion to the vertical forces at these points. I have set up the differential equations for the body in the usual way and have written the equations for the motion of the links. The problem I have is how to formulate the link force and moment equations so that they are solved using a Matlab ODE at the same time as the body motion.

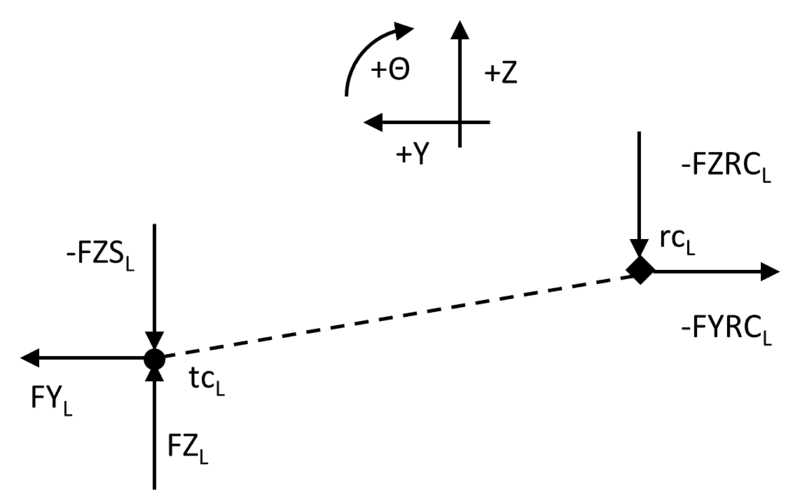
The free body diagram for the left link is below, as an example. The suspension force FZSL is described in terms of the body motion, so I think this should be solvable. The points rc and tc are also described by the body motion and, consequently, FZRCL and FYRCL are scaled in proportion to the angle between the link and the ground (that is to say, their resultant is parallel to the link but their magnitudes are unknown). So, the remaining four forces need to be solved, but these are directly a function of FYL, which is a function of FZL, through the statics equations.

The problem I seem to have is finding a way of arranging the static equations for each link so that they are written in terms of the body motion. However, each attempt I make to rearrange them fails to do this. I perhaps have too many unknowns and not enough solvable equations.

The body equations are:

maY=FYRCL+FYRCR

maZ=FZSL+FZSR+FZRCL+FZRCR–FZW

IXθ¨X=FZSL⋅tcyL−FZSR⋅tcyR+FYRCL⋅(cgz−rczL)+FYRCR⋅(cgz−rczR)

The equations for the left link are (taking moments about rc):

FYL+FYRCL=0

FZL+FZSL+FZRCL=0

FYL⋅rczL+FZSL⋅tcyL+FZL⋅tcyL=0

The equations for the right link are similar.

The input to the system is FY, and:

FYL=FY⋅(FZL/(FZL+FZR))

FYR=FY−FZL

Sorry for the longwinded post but I’d be very grateful for any direction you could give.

Thanks.

 

[Lnewqban]

Welcome!
Would you mind to explain a little more what is the meaning of the r-t links?

 

[jack action]

I think you are missing the equations for the spring forces ($FZS = K\Delta S$). You have to monitor where the end points of the springs are.

 

[s_aldworth]

Welcome!
Would you mind to explain a little more what is the meaning of the r-t links?

Thanks for the welcome.

Any vehicle suspension mechanism can be represented at any instant in time by a single virtual link that connects the tyre contact patch centre (tc) to the body. Although in reality it's a 3D link it is often dealt with in two separate planes - the side view and the front view. It connects to the body at the instantaneous centre, which is therefore the point at which any force in the link enters the body.

However, it is common to translate the force from the instantaneous centre to the misnamed 'roll centre' (rc) which, as it always lies under the CG, results in a force with a vertical component that can only act to raise or lower the body (referred to as jacking) and a lateral component that accelerates the body sideways and causes a body roll moment. This roll moment is reacted by the suspension's spring elements.

The point rc lies on the line between tc and the instantaneous centre. So, the two principal ways in which load is transferred from one side of a vehicle to the other are through the links and through the spring elements.

Two other contributors to weight transfer are via the unsprung mass (not included in my model) and via the lateral translation of the CG towards one side of the vehicle (included in my model). As the links tc-rc are instantaneous, you need a description of the way they change with body position so that at every instant the model is solved the current body position defines the position of tc and rc.

Hope that is clear but please let me know if more detail is required.

 

[s_aldworth]

I think you are missing the equations for the spring forces ($FZS = K\Delta S$). You have to monitor where the end points of the springs are.

They are described in paragraph 2 (first sentence) and paragraph 4 (second sentence). The forces are FZSL and FZSR shown in the body vertical and moment equations and, in the case of FZSL, in the link vertical and moment equations. It's not just springs in the model, but anti-roll bars and dampers too (it's a dynamic model).

 

[Lnewqban]

... Hope that is clear but please let me know if more detail is required.

Thank you very much.
What determines the vertical position of each rc point?

 

[s_aldworth]

Thank you very much.
What determines the vertical position of each rc point?

As I described in my first reply to you, the rc point lies on the line between tc and the instantaneous centre and underneath the CG.

 

[Lnewqban]

As I described in my first reply to you, the rc point lies on the line between tc and the instantaneous centre and underneath the CG.

Yes, but why?
What is the location of the instantaneous center?

 

[jack action]

They are described in paragraph 2 (first sentence) and paragraph 4 (second sentence). The forces are FZSL and FZSR shown in the body vertical and moment equations and, in the case of FZSL, in the link vertical and moment equations. It's not just springs in the model, but anti-roll bars and dampers too (it's a dynamic model).

They are not described, that's my point. You need equations to describe them. They depend on both position (springs & anti-roll bars) and velocity (dampers). You only have acceleration in your equations.

How do you know the values of FZSL & FZSR dynamically without following the position and velocity? I mean the basic equation should be:
$$m\ddot{x} + c\dot{x} + kx = F(t)$$
You have:
$$m\ddot{x} = F(t)$$
From my point of view, you have 11 equations and 14 unknowns, as presented in the OP:

1. aY
2. FYRCL
3. FYRCR
4. aZ
5. FZSL
6. FZSR
7. FZRCL
8. FZRCR
9. FZW
10. θ¨X
11. FYL
12. FZL
13. FYR
14. FZR

Find me at least 3 other equations to define the relationship between some of these.

 

[s_aldworth]

They are not described, that's my point. You need equations to describe them. They depend on both position (springs & anti-roll bars) and velocity (dampers). You only have acceleration in your equations.

How do you know the values of FZSL & FZSR dynamically without following the position and velocity? I mean the basic equation should be:
$$m\ddot{x} + c\dot{x} + kx = F(t)$$
You have:
$$m\ddot{x} = F(t)$$
From my point of view, you have 11 equations and 14 unknowns, as presented in the OP:

1. aY
2. FYRCL
3. FYRCR
4. aZ
5. FZSL
6. FZSR
7. FZRCL
8. FZRCR
9. FZW
10. θ¨X
11. FYL
12. FZL
13. FYR
14. FZR

Find me at least 3 other equations to define the relationship between some of these.

They are described, but the equations are not included in my post. I have not included everything to keep the post length down and because I am asking for help with the links, not the body.

 

[s_aldworth]

Yes, but why?
What is the location of the instantaneous center?

There isn't anything more I can say to describe the model and its parts, so I'll re-write my previous replies in a list of salient facts to see if that brings clarity:
1. The model is a planer front view of a single axle vehicle comprising a body with a suspension system on each side
2. Each suspension system is represented by an instantaneous link that runs from the tyre contact point (tc) to an instantaneous centre (not shown, and not required)
3. Each instantaneous link is described by a known polynomial which defines the lateral position of tc relative to the body as a function of the body to ground vertical displacement (in a body axis system)
4. The same polynomial can be used to define the angle between the instantaneous link and ground
5. Whilst a set of equations describing the forces and moments at the connections between the instantaneous centres and the body could easily be written, it is common practice to transfer the forces to the points where the instantaneous links intersect with a vertical line down from the CG. This is done so that the vertical components of the forces in the links serve only to raise or lower the body without causing any moments on it, whilst the lateral components act to accelerate the vehicle sideways and to generate a roll moment
6. The roll moment is reacted by the springs, anti-roll bars and dampers
7. For information: it doesn't matter where along the links the forces mentioned in point 5 are transferred to, so long as their components act on the body with the appropriate moment arms. The vertical and lateral forces and the total roll moment are the same in each case.
I think that's everything so I hope that helps.

 

[Lnewqban]

Thank you, @s_aldworth

 

[s_aldworth]

They are described, but the equations are not included in my post. I have not included everything to keep the post length down and because I am asking for help with the links, not the body.

I'll collate the full set of equations and post them here later.

 

[s_aldworth]

I'll collate the full set of equations and post them here later.

Here is a full set of equations as they stand at the moment. Body accelerations are a with a suffix for direction, velocities are v and displacements are d. Anything with a 0 in it means the static value. Various equations are needed to get things like ground to body displacement (gb), suspension displacement (su), their velocities, tyre contact motion, and so on. There are also constants for spring rate (k), anti-roll bar rate (kr) and damping rate (c). There are minor changes (and one typo correction) to the originally posted equation now that I don't need to edit them to make sense.

I understand the concept of needing to have enough equations to cover the number of unknowns, however, I have some trouble understanding how that applies to dynamic systems where one is going to rely on a solver to undertake numerical integration. Some clarity on that would be welcomed.

The body equations are (taking moments about the CG):
$$ma_Y=FYRC_L+FYRC_R$$
$$ma_Z=FZS_L+FZS_R+FZRC_L+FZRC_R-FZW$$
$$I_X (\ddot θ_X)=FZS_L*tcy_L-FZS_R*tcy_R+FYRC_L*ra_L+FYRC_R*ra_R$$
The equations for the left link are (taking moments about rc):
$$FY_L+ FYRC_L=0$$
$$FZ_L+FZS_L+FZRC_L=0$$
$$FY_L*rcz_L+FZS_L*tcy_L+FZ_L*tcy_L=0$$
The equations for the right link are (taking moments about rc):
$$FY_R+FYRC_R=0$$
$$FZ_R+FZS_R+FZRC_R=0$$
$$FY_R*rcz_R+FZS_R*tcy_R+FZ_R*tcy_R=0$$
The equation for the left suspension is:
$$FZS_L=(FS_L+FA_L+FD_L)*cos(θ_X)$$
Which is comprised of:
Spring force:
$$FS_L=k_L*su_L+FZ0_L$$
$$su_L=gb_L*cos(θ_X)$$
$$gb_L=(tcy_L-d_Y)*sin(θ_X )+(tcz_L-d_Z)*cos(θ_X)+d_Z$$
Anti-roll bar force:
$$FA_L=-kr_L*(su_L-su_R)$$
Damper force:
$$FD_L=c_L*(\dot {su}_L)$$
$$(\dot {su}_L)=(\dot {gb}_L)*cos(θ_X)$$
$$(\dot {gb}_L)=v_Z+(tcy_L-d_Y)*sin((\dot θ_X))$$
The equation for the right suspension is:
$$FZS_R=(FS_R+FA_R+FD_R)*cos(θ_X)$$
Which is comprised of:
Spring force:
$$FS_R= k_R* su_R+FZ0_R$$
$$su_R=gb_R*cos(θ_X)$$
$$gb_R=(tcy_R-d_Y)*sin(θ_X)+(tcz_R-d_Z)*cos(θ_X)+d_Z$$
Anti-roll bar force:
$$FA_R=kr_R*(su_L-su_R)$$
Damper force:
$$FD_R=c_R*(\dot {su}_R)$$
$$(\dot {su}_R)=(\dot {gb}_R)*cos(θ_X)$$
$$(\dot {gb}_R)=v_Z+(tcy_R-d_Y)*sin((\dot θ_X))$$
The equations for the left tyre contact motion are:
$$tcy_L=tcy0_L+tcy\_rel_L+d_Y$$
$$tcy\_rel_L=tcpoly(1)*10^3*-gb_L^2+tcpoly(2)*-gb_L$$
The equations for the right tyre contact motion are:
$$tcy_R=tcy0_R+tcy\_rel_R+d_Y$$
$$tcy\_rel_R=-tcpoly(1)*10^3*-gb_R^2-tcpoly(2)*-gb_R$$
The equation for the left swing arm angle is:
$$sa_L=atan(-(2*10^3*tcpoly(1)*-gb_L+tcpoly(2)))$$
The equation for the right swing arm angle is:
$$sa_R=atan(-(2*10^3*-tcpoly(1)*-gb_R-tcpoly(2)))$$
The equation for the left roll centre height is:
$$rc_L=tan(sa_L)*(d_Y-tcy_L)$$
The equation for the right roll centre height is:
$$rc_R=tan(sa_R)*(d_Y-tcy_R)$$
The equation for the left roll moment arm is:
$$ra_L=d_Z-rc_L$$
The equation for the right roll moment arm is:
$$ra_R=d_Z-rc_R$$
The input to the system is FY, and:
$$FY_L=FY*(FZ_L/(FZ_L+FZ_R))$$
$$FY_R=FY-FY_L$$

 

[jack action]

I understand the concept of needing to have enough equations to cover the number of unknowns, however, I have some trouble understanding how that applies to dynamic systems where one is going to rely on a solver to undertake numerical integration. Some clarity on that would be welcomed.

No solver will give you an answer unless you have one equation for each unknown.

I have difficulties making sense of your equations. Consider $su_L$, which is supposed to be the amount of the left spring compression ($k_L su_L$). I would see it as something like $gb_L - tcz_L$, or I don't understand what you mean by "ground-to-body-left". There seems to be a lot of sine and cosine in your equation for that distance $su_L$.

I'm not sure about your definition of $\dot{gb}_L$ also. I count 5 variables in the $gb_L$ equation that should vary with time. In your solver, just defining $\dot{gb}_L = \frac{d}{dt}(gb_L)$ should be enough.

Your equations seem to be really wrong.

 

[s_aldworth]

No solver will give you an answer unless you have one equation for each unknown.

I have difficulties making sense of your equations. Consider $su_L$, which is supposed to be the amount of the left spring compression ($k_L su_L$). I would see it as something like $gb_L - tcz_L$, or I don't understand what you mean by "ground-to-body-left". There seems to be a lot of sine and cosine in your equation for that distance $su_L$.

I'm not sure about your definition of $\dot{gb}_L$ also. I count 5 variables in the $gb_L$ equation that should vary with time. In your solver, just defining $\dot{gb}_L = \frac{d}{dt}(gb_L)$ should be enough.

Your equations seem to be really wrong.

I realize that I need one equation for each unknown. I should have been clearer: what is of interest is to know what the list of unknowns is. For a mass on springs and dampers I assume its displacement and velocity are the two unknowns of interest. Knowing the complete list of unknowns for the model would be a useful task to complete.

I'm not in the least bit surprised you don't understand all the details of the model when they haven't been explained to you. It would be unrealistic to expect you to know. However, ironing out the finer details is not the purpose of this post. My original concern remains unchanged and that is how to deal with the unknowns in the links.

The equations may seem to you to be wrong, but that doesn't mean they are.

 

[jack action]

what is of interest is to know what the list of unknowns is.

There is no such list. You define one equation and count the unknowns in it. There is more than one? Then you know you need other equations. You add another equation and you count all the unknowns once more. There are more than two? You need other equations. And so on until the numbers match.

For a mass on springs and dampers I assume its displacement and velocity are the two unknowns of interest.

and the acceleration. But maybe you want a certain response and are looking for the mass, stiffness, and damping necessary to achieve that response. A new list of unknowns.

In your equations, $FY$ could be an unknown, but you defined it as an input, so it's not. There is no list, it depends on what you are trying to accomplish and where you want to start. And it is very hard for us to identify your unknowns if we don't even understand what your variables represent.

My original concern remains unchanged and that is how to deal with the unknowns in the links.

What do you think they are?

You see, to me, $tc_L$ and $tc_R$ could be inputs to your model (the shape of the road). But, apparently, it is not to you. Or $a_Y$ could be an input and $F_Y$ would be what you are looking for. But you are apparently trying to do the opposite.

You are basically asking us: "What do I want?" We don't know. Why don't you tell us.

 

[s_aldworth]

Ok, that's not how I remember it from my solid mechanics days where we could specify the list of unknowns by studying the mechanism. I don't follow how the acceleration of the body is an unknown if you know its displacement and velocity and the forces acting on it. However...

I think that in the text I've put down so far many of your questions are already answered. For example, I've told you that $tc_L$ and $tc_R$ are defined by a known polynomial that takes the body position relative to ground as an input. So, they are not knowns but are a function of existing unknowns.

I must admit I'm a little lost as to what you want to know that I haven't already said, so I'll start by explaining how the spring force is derived, using the left side as an example. The spring force equations are:
$$FS_L=k_L*su_L+FZ0_L$$
$$su_L=gb_L*cos(θ_X)$$
$$gb_L=(tcy0_L-d_Y )*sin(θ_X )+(tcz0_L-d_Z )*cos(θ_X)+d_Z$$
Please note that $tcy_L$ has been corrected to $tcy0_L$. This was a change in my code that I had forgotten to update in my documentation. Apologies.

The first equation is the spring rate multiplied by the suspension displacement plus the static spring force. The static spring force is in the global Z direction because the spring is vertical when the model is at rest. The second equation is the suspension displacement and is derived from a parameter called ground-to-body displacement, which is always a vertical displacement. The suspension is always parallel to the body so the cosine of the roll angle is used to convert the ground-to-body displacement to suspension displacement. The third equation is the ground-to-body displacement and is derived as follows: Imagine the model at rest and with rigid suspension. Then consider the body of the model at the next position with the links positioned according to the fact that the suspension is rigid. The vertical difference between the tyre contact points and their original positions (i.e. on the ground) is the ground-to-body displacement. This definition is used by our suspension parameter measuring machines at work but I'll skip the reasons why. The point is that the polynomial that defines the way the tyre contact points move relative to the body is a function of this ground-to-body displacement and is data that I can obtain that describes the behaviour of real suspension systems. Thus, I need to use the same definition as the machines to make the polynomial useful to me. The equation is simply a rotation about the body CG by the body roll angle plus a translation to the new body CG position. This equation is only the vertical component of that sequence. So, I would say that the unknowns here are body positions Y, Z and Θ.

I take your point about the suspension velocity but I have always aimed to avoid using a gradient function, or similar, if I can specify the correct equation directly. I will check back through my notes to see how I arrived at the equation I've used. Excepting that, the damper force equations follow the pattern of the spring force equations. The anti-roll bar force is the roll stiffness multiplied by the difference between the suspension displacements.

The suspension forces are summed and then the vertical component taken using the body roll angle to get a vertical force at the tyre contact point.

The equations for the angles of the links to ground and the positions of the roll centres are only a function of the body position, via the polynomial and the ground-to-body displacement.

Going back to the FBD of the links: the suspension forces ($FZS_L$ and $FZS_R$) are described above. The remaining forces are unknown. If $FY_L$ and $FY_R$ were known then there would be no problem. However, as they are in proportion to the respective vertical forces ($FZ_L$ and $FZ_R$) at each point, they remain unknown.

I am uncertain whether I have written all that is needed to explain the problem so please let me know if more information is required.

 

[jack action]

I don't follow how the acceleration of the body is an unknown if you know its displacement and velocity and the forces acting on it.

That is because you don't understand what "unknown" means. It doesn't mean "impossible to determine", it means "It is not an input". If I say:
$$a = b + c$$
And I know that $b=3$ and $c=2$, well then $b$ and $c$ are "known inputs" and $a$ is the only "unknown" in the previous equation. Of course, $a=5$ after you resolve the equation. But it is still "one equation with one unknown", and that is why I can determine the value of $a$.

Even then, you could still consider you have 3 unknowns - $a$, $b$, $c$ - and 3 equations since $b=3$ and $c=2$ are also equations after all. This is the way you should look at your problem right now.

So the acceleration $a$ is unknown, but you know that the equations $a = \frac{dv}{dt}$ (or $a = \frac{v_{n} - v_{n-1}}{t_{n} - t_{n-1}}$) and $F=ma$ exist which may help you find it. It doesn't mean the acceleration is "known", it means you know the relationship the acceleration has with other variables like velocity, time, force, and mass.