Simple(?) parabolic dish design question

[theycallmevirgo]

TL;DR Summary

Not feeling too good, slowing me down a bit :).

I want to use this to design a parabolic (optical) mirror;

The problem is that in my application I need both D and f to be a parameter, but I need to specify f only as a perpendicular distance from D. In other words, I need to specify some f_2=f-d, and calculate d. I can't seem to come up with a way to do this without self-reference.

Thanks so much

Joe

ETA N/M it just took me an extra second. I'll post the solution shortly

ETA II Nope, sorry, still self reference problems. It's so annoying cause it seems so simple :/

ETA III Maple CAS says it's

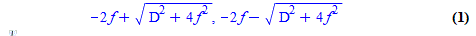
(where f=f_2)but I'll be durned if I know how it got there.

 

[Baluncore]

Specify the distance from front edge of dish to focus as g.
Then; f = d + g; d = f - g;
You specify the paraboloid size by radius; r = diameter / 2.
Given r and g, solve for parameter a of the parabola equation.
y = a * x^2

The slope of surface is; y' = 2*a*x
When 45°, slope = 1, y = f
1 = 2 * a * x
x = 1 / ( 2 * a )
f = y = a / ( 4*a^2 )
f = 1 / ( 4 * a )
For the rim of the dish.
d = a * r^2
f - g = a * r^2
f = g + ( a * r^2 )
equate the two equations for f.
g + ( a * r^2 ) = 1 / ( 4 * a )
( r^2 * a^2 ) + (g * a) - 1/4 = 0
Then solve that quadratic for the parameter a.

 

[Baluncore]

I think this is a general solution.
Specify radius of dish; r = diam / 2
Specify distance from front face of dish to focus; g
Vertex is at the origin so surface eqn; y = a · x²
Temporary; t = √ ( r² + g² ) ; which is distance from focus to lip
Parameter; a = ( t - g ) / ( 2 · r² )
Position of focus on y axis; f = 1 / ( 4 · a )
Depth of dish; d = f - g