Simple reasoning that the equivalence principle suggests curvature

[stevendaryl]

Let me try again to explain why I think that the conclusion that light should bend in a gravitational field can be made two different ways and that those two ways are equivalent (no pun intended).

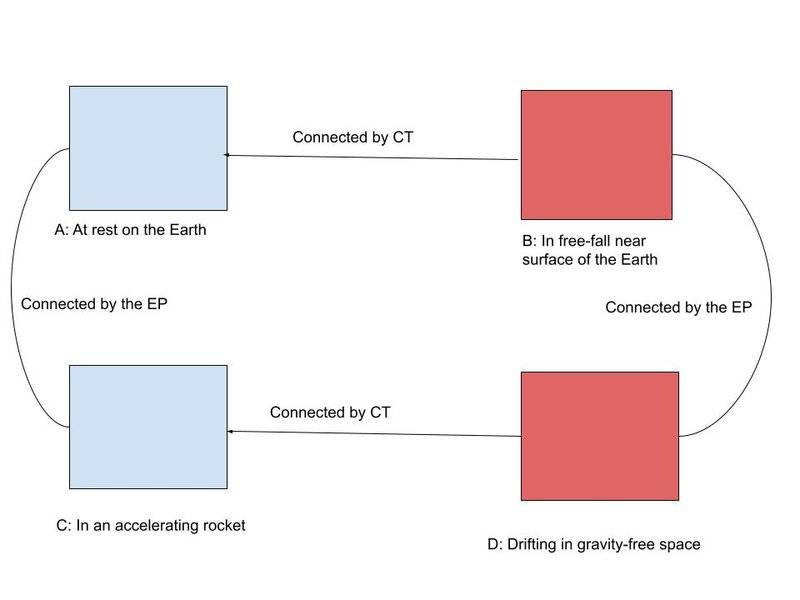
The figure below shows four different reference frames:

• A: The reference frame of someone (inside an elevator, or not) at rest on the surface of the Earth. Whether in an elevator or not, his frame only describes a small region of spacetime.
• B: The reference frame of someone (inside an elevator) in free-fall near the surface of the Earth.
• C: The reference frame of someone inside an accelerating rocket in gravity-free space.
• D: The reference frame of someone (inside an elevator, or not) drifting unaccelerated in gravity-free space.

My claim is that A and C are related to each other via the equivalence principle, and B and D are related to each other via the equivalence principle. A and B are related by a coordinate transformation, as are C and D.

For light-bending, we need to mention three coordinates: $x, y, t$, where $y$ measures location in the vertical direction, and $y$ measures location in the horizontal direction.

The two different, but equivalent, ways to get to light bending in frame A are:

Path 1: D to C to A

1. Start with D. Then we know that light initially aimed horizontally will follow the path: $x_D = c t_D$, $y_D = y_0$.
2. Transform to C. Assume that if everything is moving slowly relative to the speed of light, then we can relate the coordinates via: $t_C \approx t_D$, $x_C \approx x_D$, $y_C \approx y_D - \frac{1}{2} g t_D^2$.
3. This implies that the path of the light will be given by: $x_C \approx c t_C$, $y_C \approx y_0 - \frac{1}{2} g t_C^2$
4. Go to A using the equivalence principle. So conclude: $x_A \approx c t_A$, $y_A \approx y_0 - \frac{1}{2} g t_A^2$

Path 2: D to B to A

1. Again, start with D. Again we know that light initially aimed horizontally will follow the path: $x_D = c t_D$, $y_D = y_0$.
2. Go to B using the equivalence principle. So conclude: $x_B = c t_B$, $y_B = y_0$.
3. Transform to A. Assume that: $t_A \approx t_B$, $x_A \approx x_B$, $y_A \approx y_B - \frac{1}{2} g t_A^2$.
4. This implies that the path of the light will be given by: $x_A \approx c t_A$, $y_A \approx y_0 - \frac{1}{2} g t_A^2$

I just don't see how one is more valid than the other.

 

[PeterDonis]

This seems silly to me.

I'm not sure why, since you agree with it later on in this same post:

It's a two-part argument. The first part involves the equivalence principle.

And the second part doesn't. Which was the only point I was trying to make. As I have already said, I am not saying the argument is wrong. I am just saying that only the first part uses the equivalence principle. (Unless you want to reinterpret it as restricted to a small local patch of the curved spacetime, in which case see below.)

if we make it large enough to include the elevator, plus someone standing beside the elevator as it falls, then that's too big to be a single patch?

This just means using an accelerated frame on the same local patch, instead of the free-falling frame of the elevator. In which case, as I've already said, the EP does say you will see light bending--just as you would if you used an accelerated frame in the flat spacetime case. But you're not using any relationship to Earth, or anything else outside the patch, to make that observation. You're only using data within the small patch. You might just as well make the elevator sit at rest next to the second person, because the second person's non-inertial rest frame is really the one you're basing the argument on.

In other words, to make the argument, you have to invoke accelerated observers. And if you're going to do that, you should do it in both cases--the flat spacetime case and the local patch in curved spacetime case--if you're going to claim to be applying the EP.

The point of saying "a small patch" is that you're in a small enough region that geodesic deviation is negligible.

Yes.

 

[PeterDonis]

The two different, but equivalent, ways to get to light bending in frame A are:

I don't agree with your chart; the "connected by CT" lines say nothing about the physics, because the physics is independent of your choice of coordinates.

The fundamental physical point is that accelerated observers are different from inertial observers; they can tell the difference from their accelerometer readings. So to apply the EP, you need to have observers in both cases--flat spacetime and local patch of curved spacetime--who have the same state of motion, either accelerated or inertial. You can't invoke an accelerated observer in just one case and still claim to be applying the EP.

In short: observers A and C in your chart both observe light bending. Observers B and D don't. Those two equivalences are the ones you can use in an argument involving the EP. You can't use any equivalence between A and B, or between C and D, because they aren't equivalent: one of each pair is accelerated and the other is inertial, and this is an observable, physical difference between them that makes them not equivalent.

 

[stevendaryl]

I don't agree with your chart; the "connected by CT" lines say nothing about the physics, because the physics is independent of your choice of coordinates.

Yes, it says nothing about physics. It says something about the description of physics in an inertial versus noninertial coordinate system. The bending of light, as well as gravitational time dilation, are coordinate effects. They disappear in a local inertial Cartesian coordinate system.

In short: observers A and C in your chart both observe light bending. Observers B and D don't. Those two equivalences are the ones you can use in an argument involving the EP. You can't use any equivalence between A and B,

There is no EQUIVALENCE between A and B. That's why I didn't say that the equivalence principle relates those two reference frames. But you can relate descriptions of events in coordinate system A to descriptions of the same events in coordinate system B. It's a coordinate transformation. Whether or not A and B are "equivalent", you can use a coordinate transformation to relate their descriptions of events.

The bending of starlight and gravitational time dilation both can be understood through the following process:

Approach 1

1. Start with an analogous situation in deep space where gravity is negligible.
2. Figure out how things will work as described in an inertial coordinate system. (Reference frame D in my drawing)
3. Perform a coordinate transformation to find out how the same things would be described in the noninertial coordinate system of the rocket. (Reference frame C in my drawing)
4. Invoke the equivalence principle to find out how the analogous situation would be described in the noninertial coordinate system on a planet. (Reference frame A in my drawing)

Approach 2

1. As above. Start in deep space.
2. As above. Figure out the description in an inertial coordinate system. (Reference frame D)
3. Invoke the equivalence principle to find out how things are described by a free-falling coordinate system near the Earth. (Reference frame B)
4. Apply a coordinate transformation to find out how the same events in 3 would be described in the noninertial coordinate system on a planet (Reference frame A)

These two approaches give the SAME answer. Approximately, anyway.

 

[stevendaryl]

I'm not sure why, since you agree with it later on in this same post:

Because you're being silly. In this approach, you are NOT invoking the equivalence principle to relate (in my picture) reference frames A (a frame fixed on the surface of the Earth) and B (a free-falling frame near the Earth). You are not relating A to D (an inertial frame in gravity-free space). Frames A and B are INEQUIVALENT. Frames A and D are INEQUIVALENT. I'm not using the equivalence principle to relate A and B. I'm using a coordinate transformation. If I know how events are described in coordinate system B, and I know how to transform between the coordinate system B and the coordinate system A, then I can figure out how those same events are described in coordinate system A.

 

[A.T.]

I don't agree with your chart; the "connected by CT" lines say nothing about the physics, because the physics is independent of your choice of coordinates.

I don't understand the disagreement. How does the chart imply the opposite of what you say here?

 

[stevendaryl]

At the risk of beating a dead horse, let me try to spell everything out in excruciating detail. What we're interested in is the combination of a situation with its description in a particular coordinate system. For the bending of light, we can consider 4 situations:

1. Inertial: A light beam in an elevator floating in deep space (inertial)
2. Accelerated: A light beam in an elevator accelerating upward in deep space. (Assume that initially, there is zero velocity between these two elevators)
3. Freefall: A light beam in an elevator in freefall near the surface of the Earth.
4. Earth-fixed: A light beam in an elevator at rest on the surface of the Earth. (Assume that initially, there is zero velocity between the elevators in 3 and 4)

There are also 4 different coordinate systems:

1. Inertial: The inertial coordinate system in which the floating elevator is at rest.
2. Accelerated: The noninertial coordinate system in which the accelerating elevator is always at rest.
3. Freefall: The (local) freefall coordinate system in which the falling elevator is at rest.
4. Earth-fixed: The coordinate system in which the surface of the Earth is always at rest.

Assuming that coordinate systems are only used to describe situations in a small region of spacetime, there are 8 combinations of situation + coordinate system:

• 1A: Inertial/Inertial: Describe the path of a light beam inside a floating elevator using inertial coordinates
• 1B: Accelerated/Inertial: Describe the path of a light beam inside an accelerated elevator using inertial coordinates.
• 2A: Inertial/Accelerated: Describe the path of a light beam inside a floating elevator using noninertial coordinates.
• 2B: Accelerated/Accelerated: Describe the path of a light beam inside an accelerated elevator using noninertial coordinates.
• 3A: Freefall/Freefall: Describe the path of a light beam inside a freefalling elevator using freefall coordinates.
• 3B: Earth-fixed/Freefall: Describe the path of a light beam inside an Earth-fixed elevator using freefall coordinates.
• 4A: Freefall/Earth-fixed: Describe the path of a light beam inside a freefalling elevator using Earth-fixed coordinates.
• 4B: Earth-fixed/Earth-fixed: Describe the path of a light beam inside an Earth-fixed elevator using Earth-fixed coordinates.

Since the path of a light beam presumably doesn't depend on which elevator it is inside of (it doesn't propagate through a medium), 1A & 1B should be the same, and 2A & 2B should be the same, and 3A & 3B should be the same, and 4A&4B should be the same.

Our goal is to get to 4A/4B: The description of a light beam near the Earth using Earth-fixed coordinates.

First approach:

1. Start with 1B, the description of a light beam in an accelerated elevator using inertial coordinates.
2. Transform coordinates to get to 2B, the description of a light beam in an accelerated elevator using noninertial coordinates.
3. Invoke the equivalence principle to get to 4B.

Second approach:

1. Start with 1A, the description of a light beam in a floating elevator using inertial coordinates.
2. Invoke the equivalence principle to get to 3A, the description of a light beam in a falling elevator, described using freefall coordinates.
3. Transform coordinates to get to 4A, the description of a light beam in a falling elevator using Earth-fixed coordinates.

 

[PeterDonis]

The bending of light, as well as gravitational time dilation, are coordinate effects. They disappear in a local inertial Cartesian coordinate system.

I don't agree with this. The bending of light, locally, depends on the state of motion of the observer, which is a physical observable (just look at the reading on his accelerometer), independent of any choice of coordinates. (If we look at the bending of light globally, spacetime curvature also comes into play, but we're just restricting ourselves here to a small local patch of spacetime in which the effects of spacetime curvature can be ignored.) Similar remarks apply to "gravitational time dilation", locally.

There is no EQUIVALENCE between A and B.

Exactly. So any comparison between A and B is irrelevant to any argument that claims to use the EQUIVALENCE principle. Which you agree with:

I'm not using the equivalence principle to relate A and B.

Then you agree with my original statement that the argument @Phinrich was making is not an argument based on the equivalence principle, since his argument, like the one you have been making, relies on a relationship between A and B (or C and D in your diagram, the same thing applies to that comparison).

At the risk of beating a dead horse, let me try to spell everything out in excruciating detail.

To repeat an old saying, the problem with this discussion is that you think that, if I disagree with you, it must be because I don't understand your position.

In fact, as I have noted above, we don't disagree about many things that have come up in this thread. I do, however, disagree with some things you have said; the main one is the one I mentioned at the start of this post.

 

[cianfa72]

I think this can be translated to Lorentzian geometry, but only in the special case where all three sides of the triangle are timelike.

"Relative velocity" in this case means as measured in the locally inertial frame in which one of the two participants is at rest. Alternatively you can define in invariant way by the formula
$$
U_\alpha V^\alpha = \frac{1}{\sqrt{1 - v^2}} \quad (=\cosh \varphi)
$$
to define the relative velocity $v$ between two 4-velocities $\textbf{U}$ and $\textbf{V}$.

Reading this old thread, 4-velocities $\textbf{U}$ and $\textbf{V}$ are in some sense "invariant" since they are geometric objects. In a broader sense velocity by definition is frame-dependent, however in this context (4-velocity) is not.

Did I get it correctly ?

 

[Orodruin]

Reading this old thread, 4-velocities $\textbf{U}$ and $\textbf{V}$ are in some sense "invariant" since they are geometric objects. In a broader sense velocity by definition is frame-dependent, however in this context (4-velocity) is not.

Did I get it correctly ?

I would say relative velocity between two objects (colocated in spacetime) is not frame dependent as it can be defined through $U\cdot V = \gamma(v)$. I do not find that there is much need to talk about "separation velocity" of two objects in a local inertial frame in GR.

 

[cianfa72]

I would say relative velocity between two objects (colocated in spacetime) is not frame dependent as it can be defined through $U\cdot V = \gamma(v)$.

Yes, since the two objects are assumed to be colocated in spacetime.

However the 4-velocity itself is not frame-dependent (it is the tangent vector to a worldline and a worldline is a geometric object).

 

[Orodruin]

However the 4-velocity itself is not frame-dependent (it is the tangent vector to a worldline and a worldline is a geometric object).

I never said it was.

 

[cianfa72]

According to that post https://www.physicsforums.com/threads/simple-reasoning-that-the-equivalence-principle-suggests-curvature.1002557/#post-6487001 there is a physical procedure involving Alice, Bob and Carol to ascertain the curvature of the underlying spacetime (i.e. tidal gravity) by mean of timelike geodesics.

What about if at least one of the 3 timelike geodesics is replaced by a spacelike geodesic, is there still a similar physical interpretation ?

 

[pervect]

According to that post https://www.physicsforums.com/threads/simple-reasoning-that-the-equivalence-principle-suggests-curvature.1002557/#post-6487001 there is a physical procedure involving Alice, Bob and Carol to ascertain the curvature of the underlying spacetime (i.e. tidal gravity) by mean of timelike geodesics.

What about if at least one of the 3 timelike geodesics is replaced by a spacelike geodesic, is there still a similar physical interpretation ?

The technique as stated in that post only applies to timelike geodesics. It's closely related to a technique that works for three space-like geodesics to detect and determined the curvature of what one might term the 3d subspace spanned by the three space-like geodesics. To be as rigorous as I can be, I suppose I need to note that what we do is take a tangent space at some point P on a 4d space-time manifold, then three space-like vectors at that point P generate a 3d subspace of the 4 dimensional manifold at that point.

By using the exponential map, we essentially conflate two slightly different 3 dimensonal spaces, one is a 3d space which exists in the tangent space, and one of which exists on the manifold. These two different spaces are connected via a mapping, the exponential map.

The 3d surface in the tangent space is flat, by definitiotion, but the 3d surface defined by mapping the tangent space into the manifold via the exponential map has the possibility of being curved.

The easiest thing to measure is to consider only two space-like vectors at some point P on the manifold rather than 3. Then it genrates a 2 dimensional surface, which has a curvature that can be represented by a single number, due to the constraints on the Riemann curvature tensor.

So we draw a plane surface in the tangent space, defined by two basis vectors in the tangent space. This generates a two dimensonal surface on the manifold, and we can talk about whether or not this 2 dimensonal surface is flat or curved. The experimental procedure here would be to draw a "triangle" in the manifold whose "sides" are actually geodesics. Then we can measure the angles between the geodesics where they meet, and if the space of the 2d submanifold is flat, the sum of the interior angles will be 180 degrees. If the space of the submanifold is not flat, that sum of the interior angles will be different than 180 degrees.

Dr. Greg's post that you mentioned essentially reformulates this idea to time-like geodesics rather than spatial geodesics.

A procedure I have suggested in the past for understanding what spatial curvature means in three spatial dimensons (note that this is different from what space-time curvature means in 4 dimensions) is that we consider three orthonormal basis vectors at some point P, and consider each of the three 2 dimensonal submanifolds genrated by pairs of basis vectors.

This technique can prove that a 3d space is not flat, as if any of the 2d subspaces is not flat, the 3d space is not flat. To actually prove it is flat requires it to be refined a bit. I think that this post would get to be too long if I went into the necessary refinements, but I hope this helps clarify things somewhat.

Essentially there are 6 numbers (degree3s of freedom) of the Rieman curvature tensor, by itself the above technique only makes three of them zero, and we need all six to be zero to have no curvature.

If you're interested in more ramblings about this or other aspects of inter preting the Riemann curvature tensor accor ding to my part iclar preference, just ask.

 

[cianfa72]

The 3d surface in the tangent space is flat, by definition, but the 3d surface defined by mapping the tangent space into the manifold via the exponential map has the possibility of being curved.

Yes, this is math i.e. you are talking about vectors in tangent space and their mapping into the spacetime manifold via the exponential map.

However, in @DrGreg timelike geodesics case, there is a physical procedure to perform in order to ascertain the spacetime curvature. Here picking spacelike vectors in the tangent space at a given event A basically amounts to pick a simultaneity convention, I believe. The latter is an arbitrary choice as the geodesics we get from it.

Btw the simultaneity convention chosen cannot be quite arbitrary since events assigned to the same coordinate time must result spacelike separated from event A.