Simplest Proof of Satisfiability Under Interpration

[tragito89]

Hello,

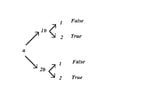
What is the easiest way to prove (or show) whether the following is true or false?

(∃x)(∃y)Rxy

Domain = { 1 , 2 }
a: 1
b: 2
R: { < 1 , 2 > , < 2 , 2 > }
H: { 1 , 2 }
K: empty setThank you.

 

[Evgeny.Makarov]

Hi, and welcome to the forum.

What you wrote is, strictly speaking, neither true nor false. You wrote a formula and an interpretation. A formula by itself is not true or false; it's just a string of characters. An interpretation is neither true nor false; it's a mathematical structure (a sequence of sets or something like that). If you ask whether the formula is true in this interpretation, that is a meaningful question. Don't you think that there exist an $x$ and a $y$ in $\{1,2\}$ such that the pair $(x,y)$ satisfies the predicate $R$?

As for the title of the thread, the phrase "satisfiability under interpretation" also sounds strange. A formula is satisfiable if there exists an interpretation where the formula is true. There is no need to add "under interpretation". On the other hand, if you have a concrete interpretation, then a formula can be either true or false in it, but not satisfiable.

 

[tragito89]

Don't you think that there exist an $x$ and a $y$ in $\{1,2\}$ such that the pair $(x,y)$ satisfies the predicate $R$?

Thank you so much for the clarifications.

I do think there exists an 'x' and 'y' in {1,2} such that the pair (x,y) satisfies the predicate 'R.' I already know the formula is true in the interpretation. I am asking if there is a simple way to demonstrate or show this, so that the same method can be used for more complicated formulas that are not immediately apparent.

 

[Evgeny.Makarov]

There is no general way of showing whether a given formula is true or false in an interpretation. For example, it took over 300 years to determine that the formula
\[
\exists n\,\exists a\,\exists b\,\exists c\;n> 2\land a^n+b^n=c^n
\]
is false on positive integers.

There are some methods for certain classes of formulas, but they are more suitable for computers than for people. In studying logic, the best method is probably to approach problems like this individually using your mathematical experience.

 

[tragito89]

There is no general way of showing whether a given formula is true or false in an interpretation.

Hmm...

Maybe the problem here is that I'm not being clear enough about what I'm asking. I'm pretty sure that there's a way to show that my original formula is true under its given interpretation. The first couple of steps involves substituting the variables 'x' and 'y' with the constants 'a' and 'b' and removing the existential quantifiers. After doing this, the result should be 'Rab.' But I just don't know what else to do after that.

Anyway, I don't want to be too much of a bother. Maybe what I'm asking is too simple to answer.

 

[Evgeny.Makarov]

I'm pretty sure that there's a way to show that my original formula is true under its given interpretation.

There are two aspects to this problem. Mathematically it asks if the relation $\{\langle1, 2\rangle,\langle2, 2\rangle\}$ is true on some pair from $\{1,2\}$. This is completely obvious. From the standpoint of mathematical logic, the problem asks for a correct use of the definition of when a formula is true in an interpretation. Ultimately, this also reduces to the first, mathematical, sense, but logic requires handling correctly some bookkeeping.

The first couple of steps involves substituting the variables 'x' and 'y' with the constants 'a' and 'b' and removing the existential quantifiers.

There are no constants $a$ and $b$ in your problem as it is written in post #1.

But I just don't know what else to do after that.

You need to study and understand the definition of when a formula is true in an interpretation. It may involve a valuation (a mapping from variables to the domain of an interpretation) or the concept of substitution. There are several slightly different ways to do it, so you need to consult your textbook or lecture notes. Ideally go through several examples. Feel free to post the definition (or any questions about it) so that we can write a formal solution.

 

[tragito89]

It may involve a valuation (a mapping from variables to the domain of an interpretation) or the concept of substitution. There are several slightly different ways to do it, so you need to consult your textbook or lecture notes. Ideally go through several examples. Feel free to post the definition (or any questions about it) so that we can write a formal solution.

Alright. First off, thanks for putting up with me.

I think I found what I was referring to (although I have no idea what it's called):

View attachment 4774

According to this, the formula "Rab" is true in the interpretation I mentioned because it is true under one instance of the a-variant and one instance of the b-variant. That much I can see. However, looking at the above image, I don't understand how they managed to get "False" for some instances and "True" for the others. There were a total of four possibilities (false,true,false,tree) shown here, and I don't understand where each of those results came from.

I hope what I'm asking is making more sense now.

 

[Evgeny.Makarov]

Sorry for a pause.

I don't understand how they managed to get "False" for some instances and "True" for the others. There were a total of four possibilities (false,true,false,tree) shown here, and I don't understand where each of those results came from.

Since $x,y\in\{1,2\}$, there are four possible pairs of values of $x$ and $y$:

$x=1;\ y=1$
$x=1;\ y=2$
$x=2;\ y=1$
$x=2;\ y=2$

Your picture, which renames $x$ and $y$ into $a$ and $b$, shows these variants graphically: there are two variants for $a$ ($a=1$ and $a=2$), and for each of them there are two similar variants for $b$. Since $R=\{\langle1,2\rangle,\langle2,2\rangle\}$, only two of those four variants satisfy $R$, namely, $a=1, b=2$ and $a=2,b=2$. For other values of $a$ and $b$, for example, for $a=b=1$, the formula $Rab$ is false since $\langle1,1\rangle\notin R$.

 

[tragito89]

Ah...

Thank you so much.