Simplex Method to Linear Programming

[cyeokpeng]

Solve this LP model using the Simplex method
Maximize Z = 10x1 + 12x2 + 7x3
Subject to:
20x1 + 15x2 + 10x3 <= 300
10x1 + 5x2 <= 100
x1 + 2x3 <= 50

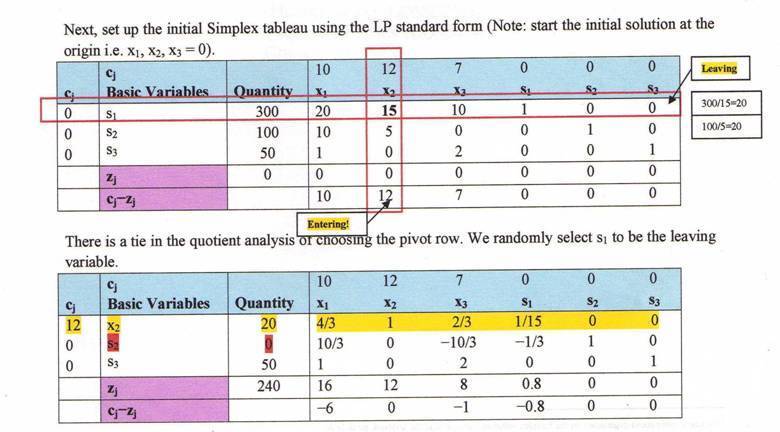
The above is my scanned work from one of the assignment files, don't know how to set up tables here.
Hopefully I didn't make any careless errors.
The final tableau shows a degenerate solution, due to the tie in the pivot row, causing value of zero in the other unchosen basic variable s2. But from what I have learned from the text, degeneracy will cause you to loop back to the same solution, but this solution somehow don't loop. Did I make a mistake, or is it actually a normal situation? My answer reports that final tableau as the optimal solution.
i.e. x1 = 0, x2 = 20, x3 = 0
giving an objective function value of Z = $240.

 

[LightHero]

The Simplex method for this LP is as follows:Step 1: Set up the initial tableau.Variables x1 x2 x3 s1 s2 RHS20x1 + 15x2 + 10x3 1 0 0 20 15 30010x1 + 5x2 0 1 0 10 5 100x1 + 2x3 1 0 1 1 2 50Z 10 12 7 0 0 0Step 2: Select the leaving variable.Since the value of the RHS column in the third row is the least negative, we select s2 as the leaving variable.Step 3: Calculate the pivot row.We calculate the pivot row by dividing each element in the third row by its corresponding element in the leaving variable column (in this case, s2).Variables x1 x2 x3 s1 s2 RHS20x1 + 15x2 + 10x3 1 0 0 20 15 30010x1 + 5x2 0 1 0 10 5 100x1 + 2x3 1/2 0 1/2 1/2 2 25Z 10 12 7 0 0 0Step 4: Select the entering variable.The entering variable is the column with the most positive ratio in the pivot row. In this case, it is x2, which has a ratio of 0.Step 5: Calculate the pivot element.The pivot element is calculated by dividing the corresponding element in the RHS column of the leaving variable row by the corresponding element in the entering variable column. In this case, the pivot element is 300/0, which is undefined.Step 6: Calculate the new tableau.We calculate the new tableau by performing elementary row operations on the previous tableau.Variables x1 x2 x3 s1 s2 RHS20x1 + 15x2 + 10x3 1 0 0 20 15

 

[Mene]

I would like to provide a response to the use of the Simplex Method in solving linear programming problems. The Simplex Method is a widely used algorithm for solving linear programming problems, and it is based on the concept of moving from one basic feasible solution to another until an optimal solution is reached.

In the given LP model, the objective is to maximize the function Z = 10x1 + 12x2 + 7x3 subject to three constraints. To solve this problem using the Simplex Method, we need to first convert the inequalities into equations by introducing slack variables, and then set up the initial tableau. The initial tableau for this problem would look like this:

| Basis | x1 | x2 | x3 | s1 | s2 | s3 | RHS |
|-------|----|----|----|----|----|----|-----|
| s1 | 20 | 15 | 10 | 1 | 0 | 0 | 300 |
| s2 | 10 | 5 | 0 | 0 | 1 | 0 | 100 |
| s3 | 1 | 0 | 2 | 0 | 0 | 1 | 50 |
| Z | -10| -12| -7 | 0 | 0 | 0 | 0 |

The first step in the Simplex Method is to identify the pivot column, which is the column with the most negative coefficient in the Z row. In this case, it is the x1 column. Then, we need to identify the pivot row, which is the row with the smallest positive ratio of the RHS to the pivot column coefficient. In this case, it is the s2 row, with a ratio of 100/10 = 10.

Next, we perform row operations to make the pivot element (10 in this case) equal to 1 and all other elements in the pivot column equal to 0. This results in the following tableau:

| Basis | x1 | x2 | x3 | s1 | s2 | s3 | RHS |
|-------|----|----|----|----|----|----|-----|
| s1 | 2 | 3 | 1 | 1/10| 0