Simplified rocket lateral dynamics model sign convention

[Johan M]

TL;DR Summary

I would like to confirm if the sign convention for the forces present in a model is correct. It entails the linear and angular momentum for a simplified rocket model. The rocket has airfoil shaped flaps whose lift force can be used to adjust the rocket orientation

Hi everyone . I had came across a simplified simplified rocket lateral dynamics model :https://github.com/build-week/hover...n-scripts/design-scripts/jet_vane_speed.ipynb . It has vanes at the exit which generate lift force and can control the rocket orientation. In it, linear and angular momentum equations are present for the current orientation:

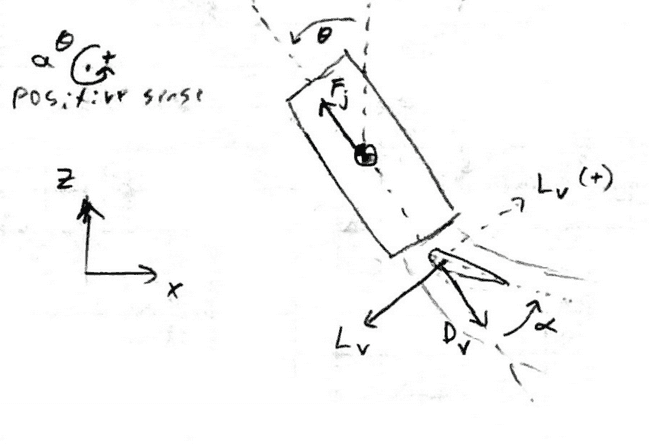
Fj: engine thrust
Lv: lift force
Dv: drag force:
alpha: vane angle of attack
theta: pitch over angle of the rocket

The angular momentum:
[IMG alt="$$
L_v r_v = I \ddot{\theta}
$$"]https://render.githubusercontent.com/render/math?math=L_v r_v = I \ddot{\theta}&mode=display[/IMG]Linear momentum:
[IMG alt="$$
-(F_j - D_v) \sin\theta + L_v \cos\theta = m \ddot{x}
$$"]https://render.githubusercontent.co..._v \cos\theta = m \ddot{x}&mode=display[/IMG]

I don't seem to understand the sign convention for the lift force generated by the vanes in these equations: at the current angle of attack, the lift force Lv would be in a south-west direction. In the equations, it seems the author took it in the north-east direction. In other words, should the equations instead read as:

-[IMG alt="$$
L_v r_v = I \ddot{\theta}
$$"]https://render.githubusercontent.com/render/math?math=L_v r_v = I \ddot{\theta}&mode=display[/IMG]
-(F_j-D_v)sin(theta)-L_vcos(theta)=m*xdottDoes anyone happen to know why he did otherwise? Any advice is appreciated

 

[Navin A S]

.The lift force generated by the vanes is acting in the direction of the rocket's motion, not against it, so the sign convention is correct as it is. The equations are written using the right-hand rule, which means that the lift force is acting in the positive direction. So if the vane angle of attack (alpha) is positive, then the lift force Lv will be in the north-east direction.