bnosam
- 148
- 0
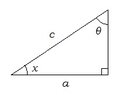
I have the expression $$sin^{-1}(cosx)$$
I'm not sure how to simplify this at all. I've never done a problem like this and it's in my textbook as a review question.
A quick boot in the right direction would help
I'm not sure how to simplify this at all. I've never done a problem like this and it's in my textbook as a review question.
A quick boot in the right direction would help
Last edited: