shamieh
- 538
- 0
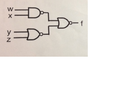
Find the simplified equation (SOP FORM) corresponding to the following circuit (i.e. apply Demorgan's theorem to bring the negations inside the parenthesis).
View attachment 1466So is it saying W NAND X which means (w!x!) + YNORZ so (w!x!) + (y!z!) = wxyz?
View attachment 1466So is it saying W NAND X which means (w!x!) + YNORZ so (w!x!) + (y!z!) = wxyz?