Simulate the temperature inside an aquarium tank

[bartlino]

TL;DR Summary

how to create a function in Python to model an electric heating element heating a tank of water

there's a website to size an aquarium heater or chiller.

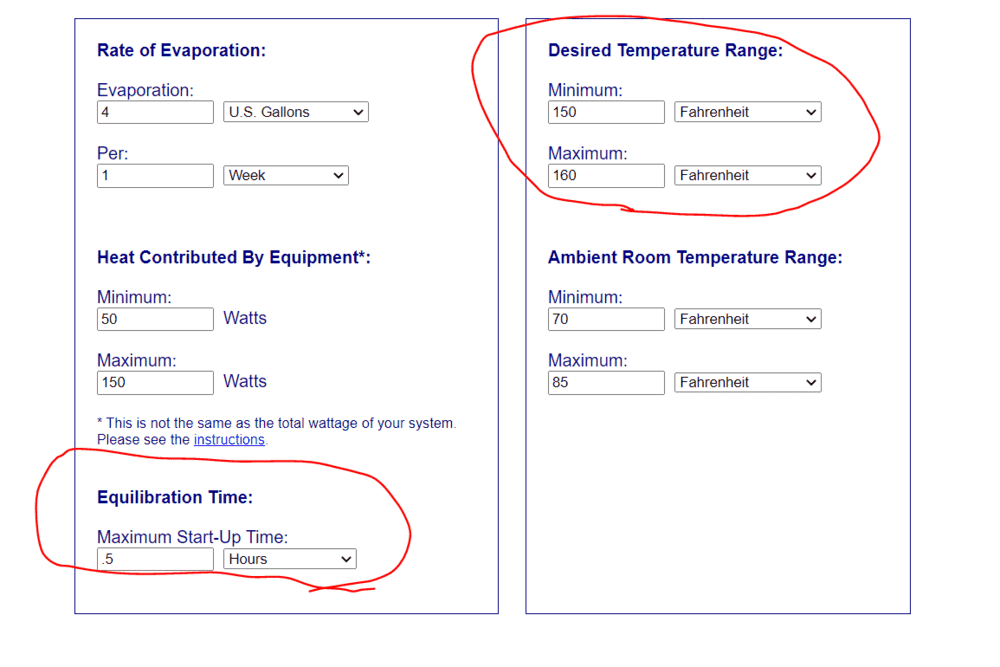
This is just for learning purposes (not for fish) but I have modified these parameters from default to perform a load calculation on a 100 gallon glass tank... For the tank temperature range I set to be between 150-160 degree F. and a startup time of .5 hours, all other parameters are left default...

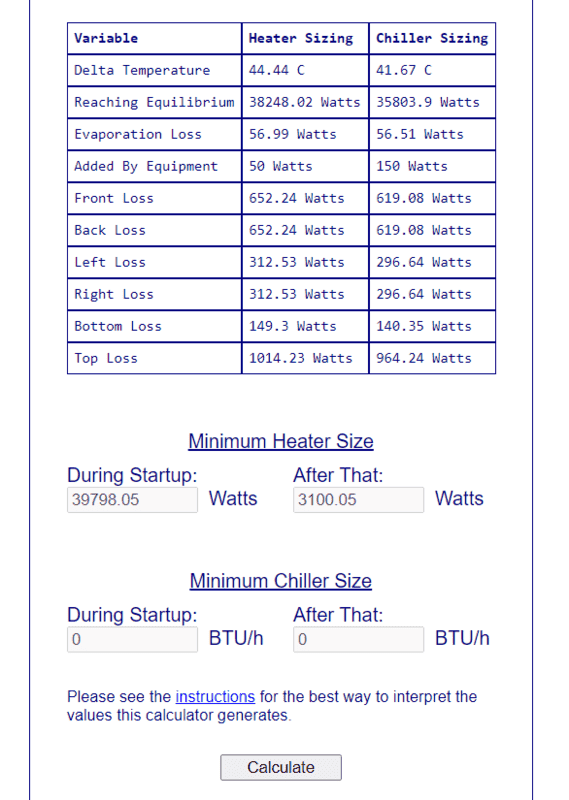
The load calc output looks like this to see all of the losses:

The question I have, is how I could I model the tank temperature over time of a 4000 watt heater cycling on and off to maintain a 150 degrees setpoint? IE, if the tank drops below 145F the heater would come on and then shut off when the tank temperature reaches 155F.

Using Python, I think I can calculate in hours how long it will take for the tank temperature to drop the 5F for when the heater would need to come on but would anyone have any tips for how I could model/calculate the tank temperature & burner cycling? (plot data over time..)

tank_volume = 100
gall_pound_conversion = 8.33
drop_in_temp = 10 #btu per pound
btu_kwh_conversion = 3413
total_loss_evap_convection = 2692/1000 #divde by 1000 to convert watts to kW

def sim():
    value = tank_volume * gall_pound_conversion
    value = value * drop_in_temp
    value = value / btu_kwh_conversion
    value = value / total_loss_evap_convection
    return valueprint(sim())
0.9066374569047897

printing the function (sim()) this yields 0.9066374569047897 which I think is in hours

 

[anorlunda]

In your table, aren't you using watts in some places there should be watt hours. The difference between power and energy in this case is vital. See my signature below.

 

[bartlino]

Any chance you could give me a tip ? The function in Python I think converts everything to hours steps I tried to follow:

1) Take the volume of the tank in gallons and multiply that value by 8.33 pounds per gallon to get pounds.

2) Multiply the result above by 10 BTU per pound which corresponds to a 10F drop in temperature for the entire tank.

3) Divide the result above by 3,413 to convert BTU to kWh of heat.

4) Divide the result above by the total rate of heat loss (kW) from evaporation and conduction. Remember 1 kW = 1000 Watts.

final result in hours for when the heating element would need energize. Ultimately I am looking to write a function that would model the tank temperature as the heating element cycles.. Thanks for any help, still learning :)

 

[Lnewqban]

I see that the delta temperature is around 111 °F, which means the air around the tank is around 40 °F, while the tank is not insulated.

This link may help some:
https://www.engineeringtoolbox.com/heat-loss-open-water-tanks-d_286.html

 

[Baluncore]

1) Take the volume of the tank in gallons and multiply that value by 8.33 pounds per gallon to get pounds.
2) Multiply the result above by 10 BTU per pound which corresponds to a 10F drop in temperature for the entire tank.
3) Divide the result above by 3,413 to convert BTU to kWh of heat.

Before posting convert all mass to kg, all temp to °C, and all volumes to litre or m³.
Eliminate the confusion. Convert everything before or outside the procedure.

You do not need °F, pounds or BTU in computations.
Water weighs 1 kg per litre, so you do not need to differentiate between gallons(US) or gallons(imp) when you use litres.