- #1
halfelven
- 10
- 0
Consider a Newtonian reflector telescope:

As you can see in the image, the little secondary mirror inside the main tube is supported by an X structure called 'spider'. The four "legs" of the spider, called 'vanes' by astronomers, are actually thin stripes of high-tensile material, usually steel, tensioned for rigidity.
Diffraction at the edges of each vane distorts the image. E.g., the image of a star (a point-like object) will show four spikes, like this (visually it's not that bad, the example image here is a bit exaggerated):

Each vane actually makes two opposite spikes, and the spikes are perpendicular to the vane. So the four vanes will make in reality 4 x 2 = 8 spikes, which are then superimposed two by two.
My question is: Is there a way to simulate numerically the diffraction spikes? Given an instrument, and vanes of a given size and thickness, calculate the intensity of the spikes in any point within the virtual image. I would be satisfied with calculating the spikes produced by even a single vane, or by two opposite vanes forming a full diameter. It's okay to ignore the diffraction produced by the secondary mirror.
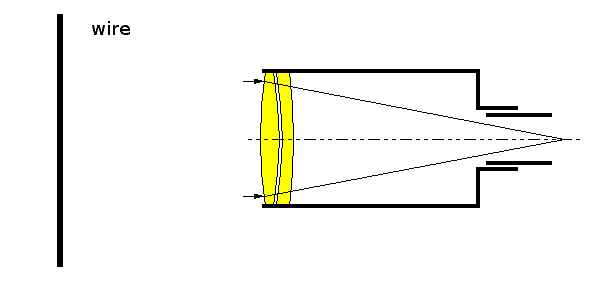
Basically, this is a regular telescope (actual type doesn't matter, it could be simulated as either reflector or refractor), with a thin and long wire intersecting the field of view at some distance ahead of it. The distance between wire and primary lens or mirror is almost equal to the focal length of that lens or mirror (at least that's the case with most Newtonian telescopes); let's say the wire-to-telescope distance is about 80% the focal length of the primary lens. The diameter of the primary lens is about 1/6 of its focal length. The telescope is looking at a point-like object at infinity, right in the center of the view field. Now calculate the diffraction effects due to the wire, as seen in the virtual image produced by the telescope, assuming various values for the wire thickness. Producing an intensity map for the diffraction effects would be great.
Slightly modified: I believe (please correct me if I'm wrong) it is enough to calculate the real image formed in the focal plane of the primary mirror or lens. There's no need to simulate a full telescope with a virtual image at infinity. The ocular merely magnifies the real image it sees in the primary focal plane, where diffraction is already spiking the image.
Simulating diffraction from the edge of the primary lens or mirror would be a nice bonus (a.k.a. the Airy rings, for a more realistic simulation), but it's not essential.
The reason I'm asking: It is generally accepted within the community of amateur astronomers that the thicker the vanes, the more intense the spikes, therefore thinner vanes are seen as "better", leading to an arms race towards ever more fragile designs. I don't think that assumption is true. Diffraction is an edge phenomenon, why should it matter what is the distance between the two edges of a vane (thickness)? A thick vane should merely block a little more incoming light, that's all. The two edges should always diffract the same amount of light, no matter what is the distance between them. But this belief is so strong, persistent, and wide spread that only a rigorous numerical simulation may stand a chance to repel it (or confirm it, in case my intuition is wrong).
I assume some kind of numerical analysis software will be needed, such as Matlab or Octave. I'm willing to put some work into this project, but I need a start. Modifying an existing software (something close to this problem, but perhaps not identical) would be perfect. Keep in mind, Optics is not what I do for a living.
As you can see in the image, the little secondary mirror inside the main tube is supported by an X structure called 'spider'. The four "legs" of the spider, called 'vanes' by astronomers, are actually thin stripes of high-tensile material, usually steel, tensioned for rigidity.
Diffraction at the edges of each vane distorts the image. E.g., the image of a star (a point-like object) will show four spikes, like this (visually it's not that bad, the example image here is a bit exaggerated):
Each vane actually makes two opposite spikes, and the spikes are perpendicular to the vane. So the four vanes will make in reality 4 x 2 = 8 spikes, which are then superimposed two by two.
My question is: Is there a way to simulate numerically the diffraction spikes? Given an instrument, and vanes of a given size and thickness, calculate the intensity of the spikes in any point within the virtual image. I would be satisfied with calculating the spikes produced by even a single vane, or by two opposite vanes forming a full diameter. It's okay to ignore the diffraction produced by the secondary mirror.
Basically, this is a regular telescope (actual type doesn't matter, it could be simulated as either reflector or refractor), with a thin and long wire intersecting the field of view at some distance ahead of it. The distance between wire and primary lens or mirror is almost equal to the focal length of that lens or mirror (at least that's the case with most Newtonian telescopes); let's say the wire-to-telescope distance is about 80% the focal length of the primary lens. The diameter of the primary lens is about 1/6 of its focal length. The telescope is looking at a point-like object at infinity, right in the center of the view field. Now calculate the diffraction effects due to the wire, as seen in the virtual image produced by the telescope, assuming various values for the wire thickness. Producing an intensity map for the diffraction effects would be great.
Slightly modified: I believe (please correct me if I'm wrong) it is enough to calculate the real image formed in the focal plane of the primary mirror or lens. There's no need to simulate a full telescope with a virtual image at infinity. The ocular merely magnifies the real image it sees in the primary focal plane, where diffraction is already spiking the image.
Simulating diffraction from the edge of the primary lens or mirror would be a nice bonus (a.k.a. the Airy rings, for a more realistic simulation), but it's not essential.
The reason I'm asking: It is generally accepted within the community of amateur astronomers that the thicker the vanes, the more intense the spikes, therefore thinner vanes are seen as "better", leading to an arms race towards ever more fragile designs. I don't think that assumption is true. Diffraction is an edge phenomenon, why should it matter what is the distance between the two edges of a vane (thickness)? A thick vane should merely block a little more incoming light, that's all. The two edges should always diffract the same amount of light, no matter what is the distance between them. But this belief is so strong, persistent, and wide spread that only a rigorous numerical simulation may stand a chance to repel it (or confirm it, in case my intuition is wrong).
I assume some kind of numerical analysis software will be needed, such as Matlab or Octave. I'm willing to put some work into this project, but I need a start. Modifying an existing software (something close to this problem, but perhaps not identical) would be perfect. Keep in mind, Optics is not what I do for a living.