Simulink: How to fix given error for a closed loop model w/ PID controller?

[simphys]

Homework Statement

The question that is asked is basically to create a closed loop model with a PID controller. (if necessary more information on the picture)
The problem that I am encountering is an error which I don't understand and know how to fix?

Relevant Equations

not relevant

Could I get some input on how to fix this problem please? Thanks in advance!

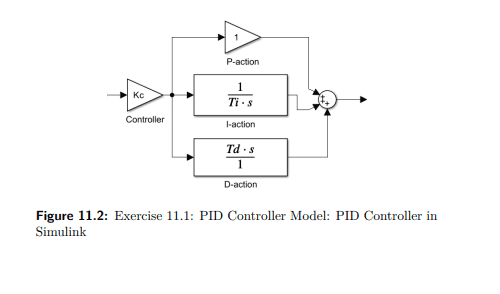
The exercise for which I need the model.

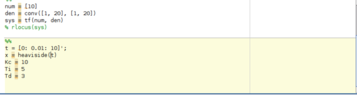
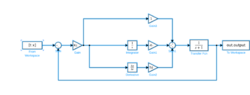
The simulink model together + the error that needs to be fixed + Matlab code used:

Note: Gain 1 = 1/Ti

 

[Tom.G]

I'm not an expert on this, but it looks like some of the equations it is solving are changing in value so fast that further calculations make no sense.

Please check the values of all the components/variables you have supplied. For instance maybe one is missing a minus sign or a decimal point. Another common problem is that an 'm' was entered instead of 'M' (or the other way around -- one means milli-, the other Mega-).

Then try changing the time step or error band, as the Error Msg. suggested.

Good Luck,
Tom

p.s. please keep us posted on what you find that works.