Jarek 31
- 157
- 31
- TL;DR Summary
- Sine-Gordon is relatively trivial model which seems to contain nearly entire SRT - are these proper intuitions? Maybe it is worth to use it in SRT education?
Sine-Gordon model is looking trivial 1D model: just
$$\phi_{tt} = \phi_{xx}-\sin(\phi)$$
which has physical realization as lattice of coupled pendulums, e.g. nice video:
Despite looking so trivial, it e.g.:
 I would like to propose a discussion about using it to understand/explain SRT, e.g.
I would like to propose a discussion about using it to understand/explain SRT, e.g.
- does it provide proper intuitions?
- which SRT phenomena can/cannot be explained this way?
- maybe it is worth to take it to SRT education (this PDE can be numerically solved) ?
$$\phi_{tt} = \phi_{xx}-\sin(\phi)$$
which has physical realization as lattice of coupled pendulums, e.g. nice video:
Despite looking so trivial, it e.g.:
- has analogues of massive particles ("kinks") corresponding to complete rotation - there is integer number of them, total number is conserved,
- these particles are created/annihilated in pairs (releasing massless excitations) - from https://en.wikipedia.org/wiki/Topological_defect#Images :
-

- there is Lorentz contraction for them - traveling kink is narrower exactly as in special relativity, mass/energy scales as in SRT:
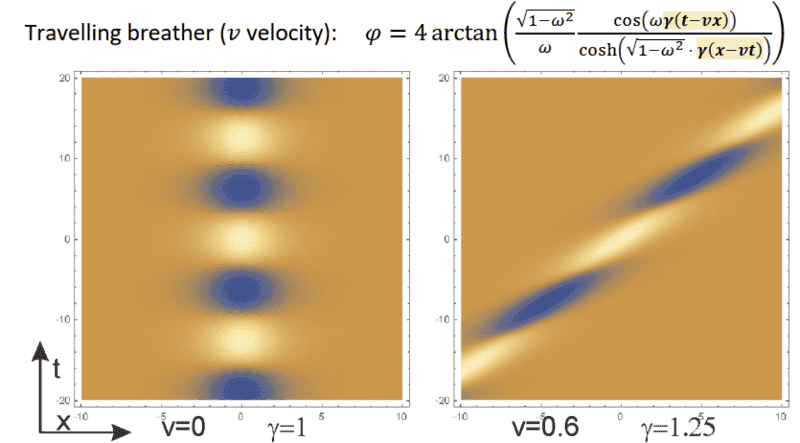
- There are oscillating solutions ( https://en.wikipedia.org/wiki/Breather ), which slow down while traveling as in SRT time dilation:
- does it provide proper intuitions?
- which SRT phenomena can/cannot be explained this way?
- maybe it is worth to take it to SRT education (this PDE can be numerically solved) ?