Single Slit Diffraction and Huygen's Principle

[bluevires]

Hey guys, We are going through single-slit diffraction recently in Physics,
I understand that using Huygen's Principle, we can treat the slit as a series of segmented wave sources, and they will interfere with each other based on their phase difference because of the path difference they traveled, this phase difference will be 0 at the central maximum position, at which point the waves interact constructively,
however, here's where the confusion starts for me,
If they are all wave sources on the same wavefront, why aren't they coherent in terms of phase difference? websites and textbook always says this

the amplitudes of the segments will have a constant phase displacement from each other, and will form segments of a circular arc when added as vectors. In this way, the single slit intensity can be constructed.

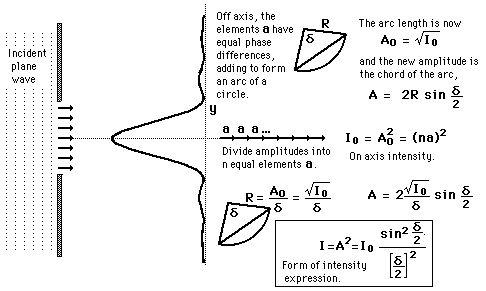
What is this vector they are adding exactly?
what does the direction represent? what does the magnitude represent? why is it circular? what does this have to do with the phase difference of the waves after they interact?

They formulated the formula for intensity of the waves based on the angle away from the central axis and the slit width as well as the wavelength of the wave being diffracted, (see the picture)

if so, how do we find the central maximum intensity? since the angle is 0.

Sorry guys I'm just really confused right now, I would appreciate it very much if you can help me out.

 

[jtbell]

What is this vector they are adding exactly?

It's a phasor ("phase vector"). Its magnitude is the amplitude of a wave, and its direction represents the phase of the wave. If you have a wave or oscillation given by

$$y = A \cos (\omega t + \phi)$$

the phasor has magnitude A and direction $\phi$. You can add waves by adding their corresponding phasors. The resultant phasor has the amplitude and phase of the resultant wave.

To add together a lot of waves from small sections of the slit, you add a lot of tiny phasors together. Graphically, you put the phasors head to tail, just like adding regular vectors. Each phasor's direction differs only slightly from its "neighbors", so the resulting chain of phasors forms a pretty smooth curve, in this case part of a circle.