Clemencio
- 4
- 1
- TL;DR Summary
- Single Slit Diffraction
Hi everyone.
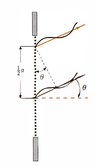
I'm studying single-slit diffraction, and a question came up: to derivate the relation for the minima (dark fringes), the slit is devided in two parts, and it's assumed the distance between the light rays is a/2. Why is this distance chosen?
I was wondering about other options. For exemple, to take two rays at the edges of the slit (distance of "a"), or other arbitrary distance, such as 3/4.
Why should I assume that rays separated by a/2 will form the 1st diffraction minimum?
Thanks!
I'm studying single-slit diffraction, and a question came up: to derivate the relation for the minima (dark fringes), the slit is devided in two parts, and it's assumed the distance between the light rays is a/2. Why is this distance chosen?
I was wondering about other options. For exemple, to take two rays at the edges of the slit (distance of "a"), or other arbitrary distance, such as 3/4.
Why should I assume that rays separated by a/2 will form the 1st diffraction minimum?
Thanks!