- #1
MetsFan09
- 5
- 0
Homework Statement
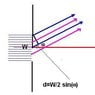
A single slit is illuminated with 660 nm and the resulting diffraction pattern is viewed on a screen 2.3 m away.
a. If the linear distance between the 1st and 2nd dark fringes of the pattern is 12 cm. What is the width of the slit?
Homework Equations
W(X/L) = m(lambda)
The Attempt at a Solution
W(.012m/.0023m = 1(660x 10^-9)
W = 1.27 x 10^-7
Someone else tells me that's wrong and that I have to divide the linear distance by two to get 6 cm instead of 12. Is this true? And if so why? I really don't understand why we would have to do that.