Sketch the region of |x-y|+|x|-|y| <= 2

[Dethrone]

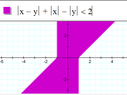
Sketch the region in the plane consisting of all points (x, y) such that $|x-y|+|x|-|y| \le 2$.

This looks like it involves the triangle inequality, but can anyone point me in the right direction? :D

 

[ineedhelpnow]

you got to solve it quadrant by quadrant

 

[Dethrone]

I think I got it!

Case 1: Quadrant 1

$x>0$, $y>0$

Subcase 1: $x>y$

$$x-y+x-y \le 2$$
$$x-2 \le y$$

Subcase 2: $y>x$
$$y-x+y+x \le 2$$
$$y \le 1$$

Continue with the other quadrants, and the answer follows :D

Edit: I just checked Wolfram Alpha...maybe I'm not (Crying)

 

[Dethrone]

Will I have to square both sides and expand? Whoops, I made an arithmetic mistake.

 

[mathbalarka]

By triangle inequality,

$$|x - y| + |x| - |y| \leq 2|x-y| \leq 2$$

Thus I get $|x - y| \leq 1$.

 

[Dethrone]

im looking at how the problem was done somewhere else. i don't think you're on the right track. your correct in terms of identifying the quadrants.
x-y+x-y>2
2x-2y>2
2(x-y)>2
x-y>1

Is it not $x-y+x-y \le 2$?

I got $x-1 \le y$

 

[ineedhelpnow]

$x \ge y$

$\left| x-y \right| + \left| x \right| - \left| y \right| = 2(x-y) \le 2$

$x-y \le 1$ which is the same as $y \ge x-1$

 

[Dethrone]

By triangle inequality,

$$|x - y| + |x| - |y| \leq 2|x-y| \leq 2$$

Thus I get $|x - y| \leq 1$.

Can you elaborate on this? (Wondering)

 

[Dethrone]

$x \ge y$

$\left| x-y \right| + \left| x \right| - \left| y \right| = 2(x-y) \le 2$

$x-y \le 1$ which is the same as $y \ge x-1$

Doing the same when $y \ge x$

We have

$$-(x-y)+x+-y \le 2$$
$$ - x + y + x - y \le 2$$
$$ 0 \le 2$$

Am I done with this quadrant, or is there more work to be done?

 

[mathbalarka]

Can you elaborate on this? (Wondering)

Well, what to elaborate? The triangle inequality gives $|x - y| \geq |x| - |y|$, no?

 

[I like Serena]

By triangle inequality,

$$|x - y| + |x| - |y| \leq 2|x-y| \leq 2$$

Thus I get $|x - y| \leq 1$.

From the triangle inequality $\big||a|-|b|\big| \le \big|a-b\big|$ we can get:
$$|x - y| + |x| - |y| \leq 2|x-y|$$
and we have the original inequality:
$$|x - y| + |x| - |y| \leq 2$$

However, if we combine them like you did, we only get a subset of the solution.

 

[mathbalarka]

I am such an idiot. I meant

$$2 \geq |x - y| + |x| - |y| \geq 2(|x| - |y|)$$

Thus, $|x| - |y| \leq 1$.

 

[I like Serena]

I am such an idiot. I meant

$$2 \geq |x - y| + |x| - |y| \geq 2(|x| - |y|)$$

Thus, $|x| - |y| \leq 1$.

This is another application of the same triangle inequality.
Any point in the solution will satisfy that inequality.

However, that only means that it is a super-set of the solution.
Still not the solution itself.To properly find the solution, I believe we have to go through the quadrants one by one.
The triangle inequalities do not really help, because they do not give a conclusive solution.

We can skip 2 quadrants though, since the solution will be point-symmetric.
That is, $(x,y)$ is a point in the solution if and only if $(-x,-y)$ is in the solution.

 

[mathbalarka]

However, that only means that it is a super-set of the solution. Still not the solution itself.

I was aware of that. I am just stating what I intended to write in the first post.

I reckon there is no smart way to find the solutions :p

 

[I like Serena]

Am I done with this quadrant, or is there more work to be done?

Yep.
You are done with the first quadrant. ;)

 

[RLBrown]

Should look like this:

Spoiler

View attachment 3214