Skewed Generalized Gaussian Distribution

[geo101]

I am looking for more information (e.g., reference, the CDF and descriptive stats) about a four-parameter skewed generalized Gaussian (SGG) distribution. I have come across the PDF for this distribution, but with no reference and not a lot of other information. Here is a snippet...

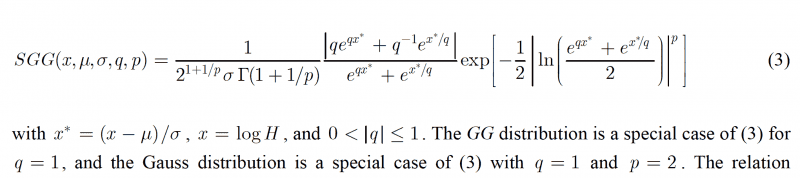
On Wikipedia, there are two forms of three parameter generalized Gaussian distributions (http://en.wikipedia.org/wiki/Generalized_normal_distribution). One that controls kurtosis, the other, essentially, skewness.

I'm wondering if anyone here can point me in the right direction for sourcing this PDF and more information about it (e.g., the CDF and descriptive stats).

Cheers
Geo101

 

[Stephen Tashi]

I'm unfamilar with that distribution, but here are some things to try if you get desperate.

Reveal the title of the article or book you quoted. Post more of it. If the article or book you quoted lists any references at all, list a few. Perhaps a forum member with access to one of the references can find something about the distribution.

Ask in the programming section if any user of Mathematica (or other symbolic math packages) can use it to compute the things you need.

Consider whether the 4-parameter distribution can be viewed as a tranformation of the data. For example the log-normal distribution can be viewed as tranforming the data by taking a logarithm and then saying the transformed data is normally distributed. The Wikipedia article on the two types of 3-parameter gaussians isn't enlightening in that respect.

It might help to ask a less imposing question! People might jump into answer a general question such as "Can probability distributions given by a family of functions with several parameters be expressed as a family of distributions defined by a few of the parameters applied to data which has been transformed by a function defined by the other parameters?" For example, the family of normal distributions can be regarded as a zero-parameter family of functions consisting of the standard normal distribution with mean 0 and variance 1 applied to transformed data. We could regard \mu and \sigma as parameters used in transforming a datum x to \frac{x - \mu}{\sigma}.

 

[geo101]

Hi Stephen

Thanks for the reply. This distribution was used is a piece of software and the previous snippet was from the manual. I have tracked it back to the original publication and it looks like the author derived it themselves. You were right, though, it appears that they have started from the General Gaussian (version 1in the wiki link in my first post) and transformed the variables to derive what they call the "Skewed Generalized Gaussian".

Here is a snippet form the original paper (full version found here...
http://onlinelibrary.wiley.com/doi/10.1029/2002JB002023/abstract)

By setting q = 1 in the above and comparing the last exponential term with that of the Generalized Gaussian (GG) it seems that "p" as used is equivalent to beta in the GG and that 2*sigma is equivalent to alpha in the GG.

I guess my question now becomes, can anyone help me determine what the transformation is and what the transformed CDF would be?

I have also emailed the original author, so if I hear back I'll post it here.

Cheers

Edit: the references they give appear only to reference the General Gaussian distribution.
Evans, M., N. Hastings, and B. Peacock, Statistical Distributions, John Wiley, New York, 2000