Skin depth of multilayered (2-layer) wire

[tm64]

Homework Statement:: Not a specific question, more just a conceptual clarification for a project. But generally:

What is an equation for the effective skin depth of a multilayered (in this case only 2 layers) wire, as a function of the resistivities and relative permeabilities of both of the materials, as well as the frequency of the current?
Relevant Equations:: See below

[Mentor Note -- Thread moved from the schoolwork forums because it is not homework-specific]

I found that skin depth can be approximated as

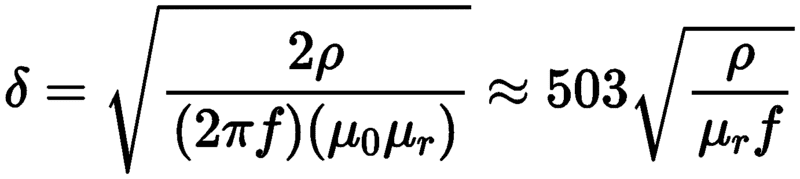
for good conductors at relatively low frequencies

But what if the conductor in question has multiple layers (say, for example, the surface had begun to oxidize)?

It seems that if the skin depth of the outer layer of the conductor is less than the thickness of said material, the overall skin depth would just be that one skin depth (please correct me if this is wrong, though).
But how can I calculate the effective overall skin depth if it's deeper than the thickness of the outer material?

Additionally, is there a way to quantify the shielding effect this outer layer has?

I would appreciate if the answer would be only in terms of these given variables and constants (i.e., resistivity, relative permeability, and frequency)

This is more of an open-ended question for a project I'm working on, so any background info, clarifications, or suggested references would also be appreciated

Thanks

 

[berkeman]

But what if the conductor in question has multiple layers (say, for example, the surface had begun to oxidize)?

Welcome to PhysicsForums

The oxide layer that you allude to is most likely a poor conductor compared to the main wire material, so I would think it would not alter the skin depth or overall AC conductivity of the wire. Is that the main thing you are concerned with, or are there other multi-layer conductor scenarios that you are thinking of also?

 

[DaveE]

I think you just have to set up the problem as normal except that the resistivity is a function of depth in the conductor. You could start with this treatment.

http://ecee.colorado.edu/~ecen3400/Chapter%2020%20-%20The%20Skin%20Effect.pdf

But, no, I don't know the answer, nor will I calculate it. Those DEs make my head hurt. I also doubt that there is a nice general result. The answer will depend greatly on the resistivity dependence.

 

[DaveE]

https://ninercommons.uncc.edu/islandora/object/etd:666/datastream/PDF/download/citation.pdf

 

[tm64]

Welcome to PhysicsForums

The oxide layer that you allude to is most likely a poor conductor compared to the main wire material, so I would think it would not alter the skin depth or overall AC conductivity of the wire. Is that the main thing you are concerned with, or are there other multi-layer conductor scenarios that you are thinking of also?

Thanks for the reply, that makes sense. So, in this case, would the current density mostly be concentrated in the non-oxidized conductor, with a skin depth similar to that as if the oxide layer weren't there?
I would also be interested in the situation of the outer layer being conductive as well, but this is more out of curiosity rather than necessity for my own work.

Also, do you have any ideas on how this outer oxide layer might play into shielding from radiation (preferably from a mathematically standpoint)?

 

[tm64]

I think you just have to set up the problem as normal except that the resistivity is a function of depth in the conductor. You could start with this treatment.

http://ecee.colorado.edu/~ecen3400/Chapter%2020%20-%20The%20Skin%20Effect.pdf

But, no, I don't know the answer, nor will I calculate it. Those DEs make my head hurt. I also doubt that there is a nice general result. The answer will depend greatly on the resistivity dependence.

Interesting idea, I'll definitely take a look into that. And yeah, a lot of this math does look pretty gnarly unfortunately. I'm trying to think of a way to model it computationally, perhaps that will make things a bit more straightforward, but I'll have to put more thought into it. Thanks for the reply

 

[tm64]

https://ninercommons.uncc.edu/islandora/object/etd:666/datastream/PDF/download/citation.pdf

Yikes, that's a huge paper, but definitely seems pretty relevant. Hopefully I'll have enough time to skim through it

 

[Baluncore]

I would also be interested in the situation of the outer layer being conductive as well, but this is more out of curiosity rather than necessity for my own work.

Also, do you have any ideas on how this outer oxide layer might play into shielding from radiation (preferably from a mathematically standpoint)?

The problem with the exposed surface oxide layer on a conductor is that it has parameters developing over time, and changing with moisture content.

The surface is most probably a dielectric most of the time, so it determines the velocity factor along the cable in the same way that a dielectric insulation does on a transmission line. The current flows below the insulation, in or on the surface of the conductive metal.

The next problem is that some metals like zinc and copper form oxides that are semiconductors. It should make no difference for power lines, but for small signals on receive antennas there are non-linear effects. Use dielectric grease and tighten all the bolts.

There can be advantages in oxide formation. Litz wire has lower resistance because the individual conductors are separated. Oxidation of multi-strand copper wire can reduce resistance at about 500 kHz, but any moisture that remains will increase the dielectric losses.

 

[tech99]

There seem to be two approaches to skin effect. In the first, we consider the magnetic field surrounding the wire and we notice that the closer to the centre we are, the stronger the field. This means that there is more inductance near the centre of the wire and this encourages current to flow on the surface.
The second method considers a wave hitting the conductor, and looks at its propagation into the conductor, which is very slow and with very great attenuation. For a dielectric layer the modification seems small, but for a conductive layer the modification seems very large.
If a dielectric layer is thick, similar to the wavelength, then we have the colour, or frequency selective effects seen, for instance, when we anneal iron.
In his investigation of single wire transmission lines, Guobau surprisingly uses a thin dielectric coating to help guide a wave. https://en.wikipedia.org/wiki/Goubau_line

 

[Baluncore]

In the first, we consider the magnetic field surrounding the wire and we notice that the closer to the centre we are, the stronger the field. This means that there is more inductance near the centre of the wire and this encourages current to flow on the surface.

Filaments of current flowing along a surface are not coupled to the same extent that the same total current would be if it flowed along only one axial filament. That is why thin wires are more inductive, while thick wires, sheets and wide flat straps have lower inductance.

The second method considers a wave hitting the conductor, and looks at its propagation into the conductor, which is very slow and with very great attenuation.

When a wave is incident on a conductive surface, the magnetic component induces a perpendicular current in the conductor. That current generates another perpendicular magnetic component, opposite to the original. Those opposites largely cancel into the conductor, so most of the incident energy is in the reflected wave.
Any current that diffuses into the conductor to more than a skin depth will be out of phase and lost as heat in the resistance of the conductor.