Sliding Rings on Rods: Solving for Inextensible String Velocity

[Saitama]

Homework Statement

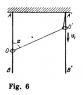
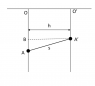
(see attachment)

Homework Equations

The Attempt at a Solution

I am not sure about this but as the string is inextensible, the component of velocity of the rings along the string should be equal. O' moves downwards and O moves upwards (not sure but it looks so). Hence, $v_1\cos \alpha=v_2\cos \alpha \Rightarrow v_1=v_2$ but this is apparently wrong.

 

[voko]

There are a couple of equations that relate the positions of the rings with the length of the string and the distance between the poles. Write them down, use them to find the velocity of O.

 

[Saitama]

There are a couple of equations that relate the positions of the rings with the length of the string and the distance between the poles. Write them down, use them to find the velocity of O.

Position from where? Should I fix the co-ordinate system with origin at A?

 

[haruspex]

Suppose the string has length s and the rods are distance h apart. When O'A' = x, what is the distance OA?

 

[Saitama]

Suppose the string has length s and the rods are distance h apart. When O'A' = x, what is the distance OA?

$OA=x+\sqrt{s^2-h^2}$?

 

[voko]

$OA=x+\sqrt{s^2-h^2}$?

How come OA grows infinitely as x increases?

 

[Saitama]

How come OA grows infinitely as x increases?

See attachment.
$OA=OB+BA \Rightarrow OA=x+\sqrt{s^2-h^2}$

Why is it wrong?

 

[voko]

How come BA is fixed? Surely as x grows, it should get smaller, because the string is inextensible.

 

[judas_priest]

It cannot be v1=v2.
Here's why:
Assume the distance between the two poles as 'x' and the string length 's', the distance to be traveled by O' to reach the height of O will be √(s^2-x^2). Now, as s tends to x (i.e the ring O' starts to reach height of the ring O, it will already have a velocity, whereas O will remain to be at rest till O' lowers and starts pulling O.
Therefore, V1>V2
You can try using trigonometric ratios to prove the same.
i.e
Sin(90-alpha) = √(s^2-h^2)/(s^2)

 

[haruspex]

See attachment.
$OA=OB+BA \Rightarrow OA=x+\sqrt{s^2-h^2}$

Why is it wrong?

Because s is not equal to the hypotenuse, OO'. The string runs from O to A' via O'..

 

[Saitama]

Because s is not equal to the hypotenuse, OO'. The string runs from O to A' via O'..

Yep, I realized it before I went to sleep.

This time I get $OA=x+\sqrt{(s-x)^2-h^2}$.

Differentiating w.r.t time,
$$\frac{d(OA)}{dt}=v_2=\frac{dx}{dt}-\frac{(s-x)}{\sqrt{(s-x)^2+h^2}}\frac{dx}{dt}$$
$dx/dt=v_1$ and $s-x=h/\sin \alpha$, using these
$$v_2=v_1\left(1-\frac{1}{\cos \alpha}\right)=-v_1\frac{2\sin^2 \alpha/2}{\cos \alpha}$$

Is this correct?

I still don't understand what's wrong with my attempt in the first post.

 

[haruspex]

Yep, I realized it before I went to sleep.

This time I get $OA=x+\sqrt{(s-x)^2-h^2}$.

Differentiating w.r.t time,
$$\frac{d(OA)}{dt}=v_2=\frac{dx}{dt}-\frac{(s-x)}{\sqrt{(s-x)^2+h^2}}\frac{dx}{dt}$$
$dx/dt=v_1$ and $s-x=h/\sin \alpha$, using these
$$v_2=v_1\left(1-\frac{1}{\cos \alpha}\right)=-v_1\frac{2\sin^2 \alpha/2}{\cos \alpha}$$

Is this correct?

A minus turned into a plus in the middle there, but it must have been a transcription error because it came out right in the end.

I still don't understand what's wrong with my attempt in the first post.

I didn't understand your reasoning there, so I can't say where it was wrong.

 

[Saitama]

A minus turned into a plus in the middle there, but it must have been a transcription error because it came out right in the end.

I didn't understand your reasoning there, so I can't say where it was wrong.

Thank you haruspex!