- #1
PropulsionMan
- 3
- 0
Homework Statement
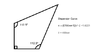
I apologize for not utilizing built-in Latex, I'll have to work with that a little more.Question statement: Explain the paths, both transmitted and reflected, that a light ray of 400nm would take if it was incident perpendicular to the bottom face ofo the crystal. If the light was in the shape below (just an arrow shown in the positive Y-direction of an X-Y coordinate plane), what would the relative orientation be when it leaves the crystal.
Homework Equations
(sin(θ1))*(n1) = (sin(θ2))*(n2) = λ1sin(θ2) = λ2sin(θ1)
The Attempt at a Solution
To be honest, I'm trying to figure out where to start with this one. I've used the provided equation and calculated n to be 1.682725, however I don't know if that corresponds to the incident or refracted side of the light, and if the light is coming in through the bottom face at the center, I'm not sure if I should consider the transmission through the assumed air medium before it hits the crystal. I could very well be overthinking it, but I'd love some direction.
Additionally, I understand that Snell's Law has the ability to predict how these light rays will trace through mediums based on wanting to take the path that's quickest through the medium. I don't know if I have to consider light that's lost at the top surface though--will some light exit the crystal?