- #36
Dank2
- 213
- 4
I haven't learn using e yet, is it possible to do it with r(cosx+isinx) ?
In other questions e can be useful, but in this question you can use both the ways and get the answer in same time( actually same efficiency)Dank2 said:I haven't learn using e yet, is it possible to do it with r(cosx+isinx) ?
It is a violation of PF rules for you to post this. You are not supposed to present solutions!Sahil Kukreja said:I have solved it
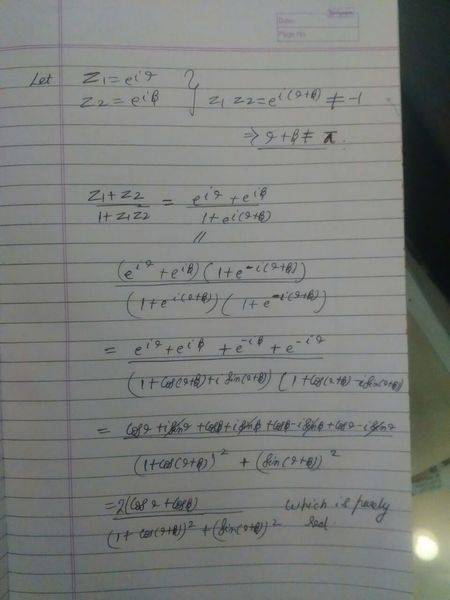
Dank2 said:I haven't learn using e yet, is it possible to do it with r(cosx+isinx) ?[/QUOT
Sahil Kukreja said:In other questions e can be useful, but in this question you can use both the ways and get the answer in same time( actually same efficiency)
it's just 4 terms that needs to be organized, cause we don't matter about the real partBvU said:Work to do, therefore ! It's almost more efficient to teach you this ##e^{i\phi}## than to drudge through all this cos sin and such...
But I can be hired to do your work if you pay better than my boss ....
Sorry. I have deleted the solution nowRay Vickson said:It is a violation of PF rules for you to post this. You are not supposed to present solutions!
Very nice! it came so smooth, thank you sir, and also, for all the others that helped . i didn't even use z1 =1/z1'.Sahil Kukreja said:I have another method to solve and it is a lot easier:- (it just solves in three steps)
Hint:-
z' --> conjugate of z
if z-z' = 0 then z is purely real
also use that since |z1|=|z2|=1
then z1=1/z1' and z2=1/z2'
its good to remember that z.z' = ## |z|^2 ##Dank2 said:Very nice! it came so smooth, thank you sir, and also, for all the others that helped . i didn't even use z1 =1/z1'.
yes i followed that, and all the terms in the numerator left was z1-z1' + z2-z2' which is ofc real, and denominator was 1+z1z2 + conjugate(z1z2), which is also real.Sahil Kukreja said:its good to remember that z.z' = ## |z|^2 ##
I learned from this too : even though you have found a way through (and I thought the ##e^{i\phi}## was pretty efficientDank2 said:Very nice! it came so smooth, thank you sir, and also, for all the others that helped . i didn't even use z1 =1/z1'.
 ) , it's good to keep an eye open for alternatives, and Sahil had no trouble pointing out a very good one !
) , it's good to keep an eye open for alternatives, and Sahil had no trouble pointing out a very good one !Dank2 said:yes i followed that, and all the terms in the numerator left was z1-z1' + z2-z2' which is ofc real, and denominator was 1+z1z2 + conjugate(z1z2), which is also real.
Ok , now i know that i had to use that z1=1/z1'Sahil Kukreja said:z1-z1' + z2-z2' is not purely real, its purely imaginary.
z=(z1+z2)/(1+z1z2)
if you put z1=1/z1' and z2=1/z2' then you must have gotten z=z'
which implies z is purely real.