- #1
axemaster
- 58
- 7
URGENT: solenoid and superconductor questions
Sorry I cross posted this, but I realized that general physics was probably a better place for it...
I have a few questions regarding the levitation of a piece of superconductor using the field from a solenoid. In other words, I want to calculate the levitation force on the superconductor as a function of distance.
Let's say I have a simple solenoid with N turns and radius R, outputting some B field at the axial distance z.
To wit: B(z)=\frac{μ_0}{4π}*\frac{2π*I*N*R^2}{(z^2+R^2)^{(3/2)}}
The superconductor is a simple loop of superconducting material, not a solid disk. It opposes any change of magnetic flux through it's looped area, so some current will flow generating a magnetic field that cancels the field of the solenoid. Starting with the z=0 case of the previous eqn, I got (note that parameters of the superconductor have subscript "s"):
B_s=-B(z)
B_s=\frac{μ_0*I_s}{2*R_s}
Thus the current in the superconductor is: I_s=\frac{2*R_s*B_s}{μ_0}
The magnetic moment of the superconductor is then:
m=I_sA
m=I_s(πR_s^2)
And the magnetic force on the superconductor due to the solenoid is:
F=∇(m*B(z))
And finally here's a graph. The B field from the solenoid is in blue, and the resulting force on the superconductor is in red. The horizontal axis is axial distance z.
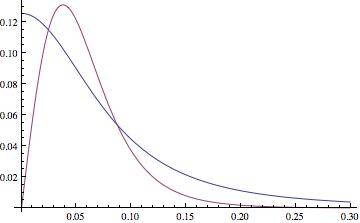
So here's my questions:
1. Is everything I did above correct? I'm aware that some of the equations are meant for far field use, but am I relatively safe in assuming that they are correct within 20% or so?
2. Am I correct in assuming that a loop of superconducting wire will behave the same as a solid disk?
3. I was a bit disturbed to notice that the expression F=m*\frac{δB(z)}{δz} goes to zero at the center of the magnet, where the magnetic field is the strongest. The force would increase up to a certain distance, then decrease as you approached the center. This seems very counterintuitive to me.
4. Having messed around with superconductors, I've noticed that one can "push" one into the field, and it doesn't seem to rebound. This seems to defy the repulsion I've calculated here. Is this a feature of Type II superconductors alone, is there something I've misunderstood, or was I imagining this effect?
5. Let's say I wanted to lift something heavy at a fairly long distance. Say, a person weighing 180lbs a foot above the ground/solenoid. That would appear to require a prohibitively powerful electromagnet. If I gave it an iron core, how much would that increase the magnetic field? If anybody has equations for this, I would be very grateful.
Sorry I cross posted this, but I realized that general physics was probably a better place for it...
I have a few questions regarding the levitation of a piece of superconductor using the field from a solenoid. In other words, I want to calculate the levitation force on the superconductor as a function of distance.
Let's say I have a simple solenoid with N turns and radius R, outputting some B field at the axial distance z.
To wit: B(z)=\frac{μ_0}{4π}*\frac{2π*I*N*R^2}{(z^2+R^2)^{(3/2)}}
The superconductor is a simple loop of superconducting material, not a solid disk. It opposes any change of magnetic flux through it's looped area, so some current will flow generating a magnetic field that cancels the field of the solenoid. Starting with the z=0 case of the previous eqn, I got (note that parameters of the superconductor have subscript "s"):
B_s=-B(z)
B_s=\frac{μ_0*I_s}{2*R_s}
Thus the current in the superconductor is: I_s=\frac{2*R_s*B_s}{μ_0}
The magnetic moment of the superconductor is then:
m=I_sA
m=I_s(πR_s^2)
And the magnetic force on the superconductor due to the solenoid is:
F=∇(m*B(z))
And finally here's a graph. The B field from the solenoid is in blue, and the resulting force on the superconductor is in red. The horizontal axis is axial distance z.
So here's my questions:
1. Is everything I did above correct? I'm aware that some of the equations are meant for far field use, but am I relatively safe in assuming that they are correct within 20% or so?
2. Am I correct in assuming that a loop of superconducting wire will behave the same as a solid disk?
3. I was a bit disturbed to notice that the expression F=m*\frac{δB(z)}{δz} goes to zero at the center of the magnet, where the magnetic field is the strongest. The force would increase up to a certain distance, then decrease as you approached the center. This seems very counterintuitive to me.
4. Having messed around with superconductors, I've noticed that one can "push" one into the field, and it doesn't seem to rebound. This seems to defy the repulsion I've calculated here. Is this a feature of Type II superconductors alone, is there something I've misunderstood, or was I imagining this effect?
5. Let's say I wanted to lift something heavy at a fairly long distance. Say, a person weighing 180lbs a foot above the ground/solenoid. That would appear to require a prohibitively powerful electromagnet. If I gave it an iron core, how much would that increase the magnetic field? If anybody has equations for this, I would be very grateful.