Solenoid Lift Force Results -- Need Data Analysis

[Albertgauss]

TL;DR

I tried out the Magnetic Force Lifting Equation with a basic solenoid setup where I lift magnets vertically into the solenoid. The small magnets only life when the current through the solenoid is large enough. The data I got does not confirm to this formula and I need some help understand my results.

Good Day,
I am trying to pick up small ferro (Neodynium)) magnets vertically with a solenoid. I want to know how much magnetic force the solenoid can pick up. The formula I tested and actual numbers for my solenoid are in the image below.

I know that the magnetic field of a solenoid is given by: B = mu_0 * N * I. I do not know how to get from this magnetic field equation to the magnetic lift force equation above, but the proofs I saw were complicated. I measure the weight of my small neodynium magnet, mg. I can measure what Force must be acting on my magnets because when I crank up the current enough, there is enough magnetic force to pull the magnets into the solenoid. Obviously, when this happens the magnetic force must just balance the gravitation weight mg of the magnet. My configuration is shown below. The magnets begin in the styrofoam under the solenoid. The slot in the styrofoam under the solenoid is hard to see, but is just under the black alligator clip and behind the red wire in the photo. I admit the setup can be improved, but this is all ball park for now.

Below is the expected force and resulting force the solenoid is predicted to exert on the magnets from the above formula

Predicted: 1 amp 3 Newtons (if you divide by 9.8, this means this solenoid should be able to pull 310 grams or so)
Actual, the solenoid was only to pick up about a 3 gram magnet
Predicted: 0.6 Amps, 1.09 Newtons, or able to pull up a 110 gram mass
Actual, the solenoid could only pick up a larger 12 gram magnet about

The magnets were all cylindrical, ~all about 1.8 inch thick, with the radius from milimeters to one centimeter or so.

You can see from my results that when I actually do this experiment, the solenoid picks up much less mass than it should, or has much less lifting force then what the equation above predicts.

Does the "Magnetic Lifting Force" equation I found apply to some other situation? It doesn't seem to work at all for a basic air-core solenoid..

What would be real engineering numbers (real-world situation) where a configuration (or the "Magnetic Lifting Force Equation" above) like this could work?

Is there some other formula that would better explain the results I got for my particular solenoid?

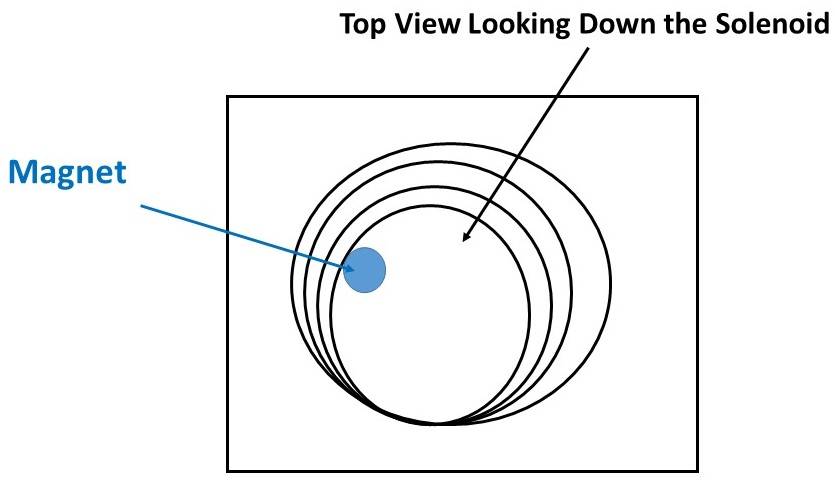
Also, it can actually be a little difficult to get the solenoid to suck up the magnets. The solenoid likes to spit them back out, not just fall out because of gravity, but actually spit back out. I know if the Neo-Dyn magnet is oriented wrong, I could get North (magnet) on North (solenoid) and South/South same way and that would cause the solenoid to spit the magnet out. When the magnets do get sucked up, they hug the wall at the bottom of the solenoid. I felt the Neo-dyn magnets should be in the center, along the solenoid axis, but this never happened. I sketch below this part, and I need help explaining what is happening.

 

[tech99]

Is it because the magnet is short. I thnk you need a long magnet so the poles are more isolated.

 

[Albertgauss]

Do you mean a longer solenoid or longer neo-dyn magnets? (Or even both) .

 

[tech99]

You already have a long solenoid, so I suggest a long magnet, of similar length.

 

[Albertgauss]

I see. I didn't think of that. I will try that.

Also, I realize something: when I tried to use paperclips or nails instead of neodyn magnets, the solenoid can attract those objects even less, that is, even larger currents are required to pick up paper clips and nails than neodyn magnets. That is, shouldn't the magnetization M of the object matter? How come M for the object to be picked up does not appear in the Magnetic Force Lifting Equation?