- #36
- 9,568
- 775
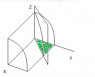
They are different parameterizations of the same circular region. If you let$$
y = r\cos\theta,~z = r\sin\theta,~ x = x$$or
$$z = r\cos\theta,~y = r\sin\theta,~ x = x$$What is different about them is they aren't the same ##\theta##. In the first case ##\theta## measures counterclockwise from the ##y## axis, and in the second case it measures clockwise from the ##z## axis, looking at the zy plane from the positive x direction.
y = r\cos\theta,~z = r\sin\theta,~ x = x$$or
$$z = r\cos\theta,~y = r\sin\theta,~ x = x$$What is different about them is they aren't the same ##\theta##. In the first case ##\theta## measures counterclockwise from the ##y## axis, and in the second case it measures clockwise from the ##z## axis, looking at the zy plane from the positive x direction.