Solid Mechanics Beam Stress Question

In summary, the "Solid Mechanics Beam Stress Question" discusses the calculation of stress in beams subjected to various loads. It emphasizes the importance of understanding beam theory, including concepts like bending moment and shear force, and how they relate to stress distribution across the beam's cross-section. The question typically requires the application of formulas derived from the principles of solid mechanics to determine the maximum stress experienced by the beam under specific loading conditions.
  • #1
Leighanne
2
0
Homework Statement
Looking for some help in solving this practice problem, I have tried multiple times and can't seem to get to the correct answers.
Relevant Equations
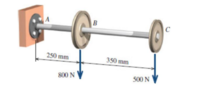
The solid 30 mm diameter steel [E = 200 GPa] shaft shown in Figure supports two pulleys. For the loading shown, use discontinuity functions to compute:

(a) the deflection of the shaft at pulley B.

(b) the deflection of the shaft at pulley C.

answers: (1.539mm, 6.15mm)
1704649582788.png
1704649574169.png
 

Attachments

  • Screenshot 2024-01-07 114117.png
    Screenshot 2024-01-07 114117.png
    14.3 KB · Views: 53
  • 1704649548546.png
    1704649548546.png
    35.6 KB · Views: 52
Physics news on Phys.org
  • #2
You are supposed to use the singularity function to find the deflections. You need to write the moment as a function of ##x##. Then the deflections come from integrating twice:

$$EI \frac{d^2y}{dx^2} = M(x)$$

Why are you trying to find the shear stress?
 
  • #3
Uploaded the wrong solution attempt whoops!
heres the correct one.
1704650460080.png
 
  • #4
Leighanne said:
Uploaded the wrong solution attempt whoops!
heres the correct one.
View attachment 338230
There should be a constant moment that you have not included in ##M(x)##. There may be more, but start there( i.e there is vertical reaction and moment at A under equilibrium).
 

FAQ: Solid Mechanics Beam Stress Question

What is the difference between bending stress and shear stress in a beam?

Bending stress occurs due to the bending moment applied to the beam, causing the material to experience tension on one side and compression on the other. Shear stress, on the other hand, arises from shear forces that act parallel to the cross-sectional area of the beam, causing layers of the material to slide against each other.

How do you calculate the maximum bending stress in a beam?

The maximum bending stress in a beam can be calculated using the formula: σ = M*c/I, where σ is the bending stress, M is the bending moment at the point of interest, c is the distance from the neutral axis to the outermost fiber, and I is the moment of inertia of the cross-sectional area about the neutral axis.

What is the significance of the neutral axis in beam stress analysis?

The neutral axis is a line within the cross-section of a beam where the material experiences zero stress during bending. It separates the tensile and compressive regions of the beam. Identifying the neutral axis is crucial for calculating bending stresses and understanding the beam's behavior under load.

How does the shape of a beam's cross-section affect its stress distribution?

The shape of a beam's cross-section significantly affects its stress distribution and overall strength. For example, I-beams have a high moment of inertia, which allows them to resist bending more effectively than rectangular or circular cross-sections. The distribution of material in the cross-section determines the beam's ability to handle stress and deformation.

What is the role of the moment of inertia in beam stress calculations?

The moment of inertia (I) is a geometric property that measures the distribution of a cross-section's area relative to an axis. It plays a crucial role in beam stress calculations because it quantifies the beam's resistance to bending. A higher moment of inertia indicates a stiffer beam that can resist bending more effectively, leading to lower bending stresses for a given load.

Similar threads

Engineering Calculating stress and strain in complex loading scenario
Replies
3
Views
1K
Engineering Understanding stress analysis of truss bridges
Replies
4
Views
2K
Engineering FEA question (stuck): Stress analysis on this Connecting Rod
Replies
3
Views
2K
Engineering Combined loading, where is the neutral axis?
Replies
11
Views
2K
Engineering An issue with these two curved beam homework problems
Replies
2
Views
1K
Is a solid cylinder considered thick or thin?
Replies
1
Views
1K
Engineering Intentional placement of additional mechanical loads in engineering
Replies
3
Views
1K
Calculate the maximum vertical point force P that this beam can sustain
Replies
1
Views
2K
Maximum and minimum tensile/compressive strain in beam
Replies
15
Views
6K
Engineering What is Poisson's ratio and how does it relate to stress and strain?
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top