Solution of a certain NxN matrix, when N->∞

[onkel_tuca]

Hello fellow nerds,

I've come across a math problem, where I'd like to find the solution vector of a NxN square matrix. It is possible to find a solution for a given N, albeit numbers in the matrix become very large for any N>>1, and numbers in the solution vector become very small. So it's not easy to compute solutions. Anyhow I realized that the components of the solution vector seem to converge and I'm asking myself if it's possible to write down the solution for N->∞.

Here's the matrix:

\begin{equation}
\begin{pmatrix}
1&-2&[-2]^2&\dots&[-2]^{N-1}\\
1&-6&[-6]^2&\dots&[-6]^{N-1}\\
1&-12&[-12]^2&\dots&[-12]^{N-1}\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
1&-N(N+1)&[-N(N+1)]^2&\dots&[-N(N+1)]^{N-1}
\end{pmatrix}
\begin{pmatrix}
a_1\\
a_3\\
a_5\\
\vdots\\
a_{2N-1}
\end{pmatrix}=
\begin{pmatrix}
1/3\\
1/5\\
1/7\\
\vdots\\
\frac 1 {2N+1}
\end{pmatrix}
\end{equation}

or:

\begin{eqnarray}
\sum_{k=1}^{N}a_{2k-1} \left[-l(l+1)\right]^{k-1}=\frac 1{2l+1}\;,
\end{eqnarray}

for all l≤N.

I'm looking for the vector a (the numbering of the index is indeed arbitrary). For instance for N=1, one finds a₁=1/3. For N=2 one finds a₁=2/5 and a₃=1/30. And so on. I already found that a₁→1/2 for N→∞. When I look at the numerical solutions, the other a_i also seem to converge slowly, see the following plot:

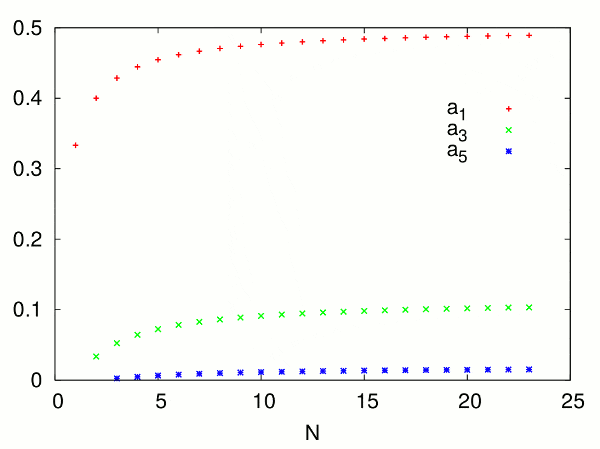
But I cannot think of a way to find these values without resorting to numerics.

Cheers, Max

 

[S.G. Janssens]

But I cannot think of a way to find these values without resorting to numerics.

Your matrix is a so-called Vandermonde matrix. A lot is known about matrices of this type, so now you have a term to search for. Since in the second column the entries are all distinct, it can be explicitly inverted, see the references in the link. (Inverting the matrix may not be the best idea, however.)

 

[onkel_tuca]

Thanks for the hint! This means I can rephrase the task to:

Find the polynomial
$$P(x)=a_1+a_3 x+a_5 x^2+...\;,$$
where
$$P(-l(l+1))=\frac 1 {2l+1}$$
for all natural l>0.
The sampling points are all on the curve
$$f(x)=\frac 1 {\sqrt{1-4x}}\;.$$