Solution to Op Amp Circuit Problem: R1=R2=R3=R5=R

[farahtc]

Homework Statement

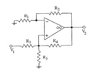
For the following circuit, sketch v2/v1 as a function of R4, if R1=R2=R3=R5=R. Also explain the behaviour of the circuit when R4=R/2.

Homework Equations

The Attempt at a Solution

After solving the circuit, i came up with v2/v1=2R4/(2R4-R). Now, if R4=R/2 , gain=infinite, is that ok? plus, what happens, when 2R4<R?

 

[unplebeian]

Assuming you have got the transfer function correct, the circuit will be unstable for values of 2R4< R.

I have got a very messy equation for the transfer function. How did you get such a clean one.

 

[unplebeian]

My transfer function is

V2/V1= (R1+R2)R4R5
--------------------------------------
R1R3R4 + R1R4R5 - R3R5R2

If all resistors are = R, then we get a gain of 2
If R4= R/2 then the gain is infinity and the opamp will saturate after a little while depending upon the slew rate of the opamp roughly speakly almost instantaneously.

 

[cepheid]

I agree with farahtc's transfer function. Assuming that all of the transients have died down, then the ideal op-amp's extremely large open-loop gain plus the negative feedback will ensure that V₊ = V_-. Since it's an easier circuit, let's solve for V_- first:

It's just a voltage divider:
$$V_- =V_2 \frac{R_1}{R_1 + R_2} = V_2\frac{R}{2R} = \frac{V_2}{2} = V_+$$

Now use Kirchoff's current law to equate the currents going into and out of the non-inverting input (I'll include the subscripts in the first line, for clarity):

$$\frac{V_1 - V_+}{R_3} + \frac{V_2 - V_+}{R_4} = \frac{V_+}{R_5}$$

$$\frac{V_1 - V_+}{R} + \frac{V_2 - V_+}{R_4} = \frac{V_+}{R}$$

put all V+ and V2 terms on the right hand side:

$$\frac{V_1}{R} = \frac{2V_+}{R} +\frac{V_+}{R_4} - \frac{V_2}{R_4}$$

$$\frac{V_1}{R} = \frac{V_2}{R} - \frac{V_2}{2R_4}$$

$$V_1 = V_2\left(1 - \frac{R}{2R_4}\right)$$

$$\frac{V_2}{V_1} = \frac{1}{1 - \frac{R}{2R_4}}$$

If R4 = R/2, then the gain is undefined (it grows arbitrarily large as R4 gets arbitrarily close to R/2). If R4 < R/2, then the gain is negative and the circuit becomes an inverting amplifier. Otherwise, the gain is positive and the amplifier is non-inverting.

 

[unplebeian]

I made a mistake in my calc's and have corrected my earlier post.

 

[unplebeian]

Hey farahtc,

I am quite sure of my answer as I even simulated it. I get a gain of 2 and infinity for your questions a and b respectively.

 

[cepheid]

If all resistors are = R, then we get a gain of 2

All resistors are not R. R4 is left as a free parameter, and part (a) asks you to sketch the gain as a function of it.

Hey farahtc,

I am quite sure of my answer as I even simulated it. I get a gain of 2 and infinity for your questions a and b respectively.

Once again, part a does not ask what the gain is when R4 = R, so I'm not sure why you're plugging that in. I'm also not sure whether you're agreeing or disagreeing with my derivation, but mine is all laid out there, and I'm quite sure it's correct. Not only that but:

1. It is in a simpler form that makes the circuit behaviour at R4 = R/2 much more transparent.
2. It was derived more easily.
3. It is equivalent to what the OP had in the first place, confirming his or her result.
4. It is probably also equivalent to your answer, since it yields the same values for R4 = R/2 and R4 = R.

What I'm trying to say is that I think that this question has been solved, and OP had it right in the first place, and simulation to confirm your result may not have been necessary.

EDIT: Although I can certainly understand your wanting to check your work and see if we were, in fact, all arriving at the same fundamental result. I have no idea how you got your answer: we must have used totally different methods. But you had it correct in the end, after all the algebra!

EDIT 2: Yeah, our answers are the same. All you have to do is plug in R1 = R2 = R3 = R5 = R into your result to end up with my result.

 

[unplebeian]

All resistors are not R. R4 is left as a free parameter, and part (a) asks you to sketch the gain as a function of it.

.

I misread the q.

What I'm trying to say is that I think that this question has been solved, and OP had it right in the first place, and simulation to confirm your result may not have been necessary.

I wanted to simulate it anyway.

EDIT 2: Yeah, our answers are the same. All you have to do is plug in R1 = R2 = R3 = R5 = R into your result to end up with my result.

Good stuff.

Thanks for your input, Cepheid.