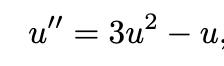Solution To Photon Trajectory Equation

[LazyPhysicist1]

TL;DR Summary

I need help solving the nonlinear photon trajectory diffeq near a mass as derived by the Schwarzschild metric.

Using the null geodesic and the Schwarzschild metric, this differential equation for photon trajectory near a mass can be derived, where u is r_s /2r:

View attachment 349924

Though this nonlinear ode is fairly easy to approximate (which I already have), I'm looking for an analytic solution or an approximate analytic solution. No online calculators work, except Wolfram (for which I don't have pro), which gives me an unusably complicated solution; https://www.wolframalpha.com/input?i=y''+=+3y^2-y

Is there a way I can better solve this differential equation/approximate an analytical solution? Thanks.

 

[ergospherical]

Without the gravitational term, the equation of motion is $u'' + u = 0$ i.e. $u \sim \sin{\phi}$, which is to say that the trajectory is a straight line (specifically $u = \tfrac{1}{b} \sin{\phi}$ if the impact parameter is $b$).

Putting in the gravitational term so that $u'' + u = 3u^2$ (with $M=1$), you take a perturbative expansion around the previous straight line solution with expansion parameter $1/b$. So to linear order,

$u = \frac{1}{b} \sin{\phi} + \frac{1}{b} \epsilon := u_0 + \frac{1}{b} \epsilon$

which you can plug back in (and use $u_0'' + u_0 = 0$) to get

$\epsilon'' + \epsilon = \frac{3}{b} \frac{1-\cos{2\phi}}{2}$

This is now a classic second order ODE for $\epsilon(\phi)$ that you can solve by finding a homogeneous and particular solution. I'll leave you to try and work out the intermediate and remaining steps.

 

[LazyPhysicist1]

Without the gravitational term, the equation of motion is $u'' + u = 0$ i.e. $u \sim \sin{\phi}$, which is to say that the trajectory is a straight line (specifically $u = \tfrac{1}{b} \sin{\phi}$ if the impact parameter is $b$).

Putting in the gravitational term so that $u'' + u = 3u^2$ (with $M=1$), you take a perturbative expansion around the previous straight line solution with expansion parameter $1/b$. So to linear order,

$u = \frac{1}{b} \sin{\phi} + \frac{1}{b} \epsilon := u_0 + \frac{1}{b} \epsilon$

which you can plug back in (and use $u_0'' + u_0 = 0$) to get

$\epsilon'' + \epsilon = \frac{3}{b} \frac{1-\cos{2\phi}}{2}$

This is now a classic second order ODE for $\epsilon(\phi)$ that you can solve by finding a homogeneous and particular solution. I'll leave you to try and work out the intermediate and remaining steps.

Thank you! I get $\epsilon = \frac{\cos{2\phi}+3}{2b} + c(\sin{\phi} + \cos{\phi})$ thus giving me a solution of

$u(\phi) = \frac{(\frac{\cos{\phi}+3}{2b} + c(\sin{\phi} + \cos{\phi}) + \sin{\phi})}{b}$, where $b=\frac{r^2 \sin ^2 \theta}{1-\frac{2 M}{r}} \frac{d \phi}{d t}$

How do I know what c is? Also, how did you get $u = \tfrac{1}{b} \sin{\phi}$ from $u = c \sin{\phi}$?

 

[ergospherical]

Also, how did you get $u = \tfrac{1}{b} \sin{\phi}$ from $u = c \sin{\phi}$?

The zero order straight line solution is $u = \tfrac{1}{b} \sin{\phi}$ because geometrically $u = 1/r$, so that's equivalent to $b = r\sin{\phi}$ (draw a sketch).

I get $\epsilon = \frac{\cos{2\phi}+3}{2b} + c(\sin{\phi} + \cos{\phi})$

Almost, but the homogeneous solution can be any linear combination of sin and cos, so they need separate coefficients. It's useful to write these in the form $C/b$ and $D/b$ so that we can explicitly keep track of the perturbative order.

$\epsilon = \frac{1}{2b} (\cos{2\phi} + 3) + \frac{C}{b} \cos{\phi} + \frac{D}{b}\sin{\phi}$

and

$u = \frac{1}{b} \sin{\phi} + \frac{1}{2b^2} (\cos{2\phi} + 3) + \frac{C}{b^2} \cos{\phi} + \frac{D}{b^2}\sin{\phi}$

Choosing $C$ and $D$ amounts to specifying the orientation of the orbit. If you want the photon to fall in from the left ($x \rightarrow -\infty$), then you want $y \rightarrow 0$ as $\phi \rightarrow \pi$ and $r \rightarrow \infty$. In this case you find $C = 2$, for example.

 

[LazyPhysicist1]

The zero order straight line solution is $u = \tfrac{1}{b} \sin{\phi}$ because geometrically $u = 1/r$, so that's equivalent to $b = r\sin{\phi}$ (draw a sketch).



Almost, but the homogeneous solution can be any linear combination of sin and cos, so they need separate coefficients. It's useful to write these in the form $C/b$ and $D/b$ so that we can explicitly keep track of the perturbative order.

$\epsilon = \frac{1}{2b} (\cos{2\phi} + 3) + \frac{C}{b} \cos{\phi} + \frac{D}{b}\sin{\phi}$

and

$u = \frac{1}{b} \sin{\phi} + \frac{1}{2b^2} (\cos{2\phi} + 3) + \frac{C}{b^2} \cos{\phi} + \frac{D}{b^2}\sin{\phi}$

Choosing $C$ and $D$ amounts to specifying the orientation of the orbit. If you want the photon to fall in from the left ($x \rightarrow -\infty$), then you want $y \rightarrow 0$ as $\phi \rightarrow \pi$ and $r \rightarrow \infty$. In this case you find $C = 2$, for example.

Got it! Thanks a lot!

 

[LazyPhysicist1]

The zero order straight line solution is $u = \tfrac{1}{b} \sin{\phi}$ because geometrically $u = 1/r$, so that's equivalent to $b = r\sin{\phi}$ (draw a sketch).



Almost, but the homogeneous solution can be any linear combination of sin and cos, so they need separate coefficients. It's useful to write these in the form $C/b$ and $D/b$ so that we can explicitly keep track of the perturbative order.

$\epsilon = \frac{1}{2b} (\cos{2\phi} + 3) + \frac{C}{b} \cos{\phi} + \frac{D}{b}\sin{\phi}$

and

$u = \frac{1}{b} \sin{\phi} + \frac{1}{2b^2} (\cos{2\phi} + 3) + \frac{C}{b^2} \cos{\phi} + \frac{D}{b^2}\sin{\phi}$

Choosing $C$ and $D$ amounts to specifying the orientation of the orbit. If you want the photon to fall in from the left ($x \rightarrow -\infty$), then you want $y \rightarrow 0$ as $\phi \rightarrow \pi$ and $r \rightarrow \infty$. In this case you find $C = 2$, for example.

How do I solve for D?

 

[ergospherical]

Another initial condition, e.g. fix the initial gradient of the light ray trajectory. In truth you don't need to do this if all you want is the first order deflection, because $(D/b^2)\sin{\theta}$ is one order smaller than the first term $(1/b)\sin{\theta}$ whatever $O(1)$ constant you pick for $D$.

 

[LazyPhysicist1]

Could you be a little more specific as to how I would determine D given initial photon direction angle a/initial gradient of light ray? I already incorporated angle a into the impact parameter.

 

[ergospherical]

You need to fix your trajectory to whatever initial conditions you want, i.e. specify a point (or a limit, e.g. infinity from the left) and a derivative along the trajectory at this point e.g. $dy/dx$ (e.g. to zero).

 

[LazyPhysicist1]

Got it, I solved for the coefficents. One last thing; do I take b as the impact parameter rsin(theta) from the nongravitational case, or $b=\frac{r^2 \sin ^2 \theta}{1-\frac{2 M}{r}} \frac{d \phi}{d t}$, which is the impact parameter in schwarzachild spacetime. Also, I take it to be the parameter for the initial condition right? Not the parameter for each point.