Solutions of the Bloch equations for MRT

[Derbyshire]

Hello all,

I have a question about the relationship between

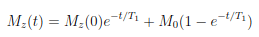
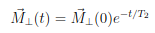
resp.

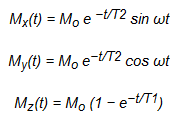
and the Bloch equations

.

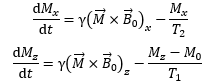Are these upper equations special solutions of the Bloch equations? If yes, under what condition(s) do the solutions hold?

Thanks in advance for helpful support!

 

[Dale]

Yes, those are the free precession equations. They apply when there is no RF being transmitted.

 

[Derbyshire]

Thank you. So the upper 5 equations are valid e.g. after the end of a 90° excitation pulse as long as no further RF pulse is irradiated?

 

[Dale]

Thank you. So the upper 5 equations are valid e.g. after the end of a 90° excitation pulse as long as no further RF pulse is irradiated?

Yes, that is right

 

[Derbyshire]

Thanks Dale,

one more question: i assume that the lower three solutions are the magnetization component from "view" of the detector coil, right?

 

[Dale]

They are basically the same. The differences are:

View attachment 330081
View attachment 330080

These assume that the spins are on-resonance so the phase of the transverse component is constant.

View attachment 330079

This assumes that the longitudinal magnetization is 0 at $t=0$ (I.e. right after a 90 deg RF pulse)

 

[Derbyshire]

Thanks!