Solve 2 Triangle Problem: Calculate Exact Value of x

[YouAreAwesome]

TL;DR Summary: My student had this in an exam. Have I solved it correctly?

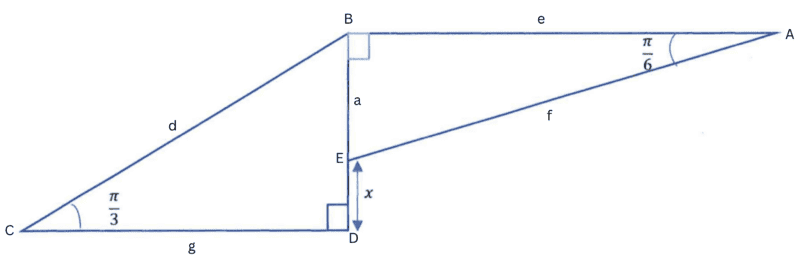
Question: Calculate the exact value of x.

First note we've not been provided any numerical lengths, therefore the expression for x will include at least two variables, one to account for the variable size of ΔCDB, and one to account for the variable size of ΔEBA.

Next note that by the angle sum of a triangle∠CBD=∠BAE meaning the triangles CDB and EBA are equiangular, and therefore similar.

My attempt is to write x in terms of the length a, and the scale factor from ΔEBA to ΔCDB of k.

In ΔCDB:
Tan(Pi/3) = (a+x)/g
g = (a+x)/√3

Now scaling ΔEBA by k to equal ΔCDB:

ka = g
ka = (a+x)/√3
ka√3 = a+x
x = ka√3-a
x = a(k√3-1)

Can someone please confirm this expression to see if I have missed a trick to simplify this even further or made a mistake somewhere? The question seems too difficult for the level my student is at and I wonder if the question is missing information.

Appreciate any input.
Cheers

 

[YouAreAwesome]

Could you explain this part further?

If one triangle can become another via resizing, then those triangles are similar.

There are Pi radians in a triangle.
In ΔCDB, Pi - Pi/2 - Pi/3 = Pi/6 which is equal to the size of an angle in ΔEBA therefore the triangles are similar (they each have a right angle and one equal angle, therefore the two triangles are equiangular - meaning all three corresponding angles are equal).

 

[pasmith]

ka = g
ka = (a+x)/√3
ka√3 = a+x
x = ka√3-a
x = a(k√3-1)

Can someone please confirm this expression to see if I have missed a trick to simplify this even further or made a mistake somewhere? The question seems too difficult for the level my student is at and I wonder if the question is missing information.

Appreciate any input.
Cheers

You should express $k$ in terms of lengths of corresoinding sides of the trangles. Alternatively, trignometry will get there directly. $$\begin{split} d\sin \frac\pi 3 &= x + f \sin \frac\pi 6 \\ \frac{\sqrt 3}{2}d &= x + \frac f 2 \\ x &= \frac{d}{2}\left(\sqrt{3} - \frac fd\right) \end{split}$$ Without further information on the lengths of the sides I think this is the best we can do.

 

[YouAreAwesome]

You should express $k$ in terms of lengths of corresponding sides of the triangles.

Thanks, makes sense.

Without further information on the lengths of the sides I think this is the best we can do.

Ok great, that is what I was thinking but I thought I may have missed something.

It makes sense to use the common side in the way you have laid it out

Cheers

 

[Lnewqban]

There are Pi radians in a triangle.
In ΔCDB, Pi - Pi/2 - Pi/3 = Pi/6 which is equal to the size of an angle in ΔEBA therefore the triangles are similar (they each have a right angle and one equal angle, therefore the two triangles are equiangular - meaning all three corresponding angles are equal).

I apologize for wasting your time with that question, which I did not delete soon enough.
I believe that the diagram has been drawn out of proportion on purpose in order to induce the confusion that I suffered after just a superficial analysis.

If the problem offers no additional constrains, its point may be simply to test the ability of the student to recognize that both triangles are similar despite both being turned and flipped respect to each other; and then, create one equation of proportionality for any pair of corresponding sides.

 

[YouAreAwesome]

I apologize for wasting your time with that question, which I did not delete soon enough.
I believe that the diagram has been drawn out of proportion on purpose in order to induce the confusion that I suffered after just a superficial analysis.

If the problem offers no additional constrains, its point may be simply to test the ability of the student to recognize that both triangles are similar despite both being turned and flipped respect to each other; and then, create one equation of proportionality for any pair of corresponding sides.

The diagram you've constructed makes the similarity visually clear. I named the triangles CDB and EBA for this purpose.

And if you are right about the point of the problem, I think it is too difficult for the age group (15/16 yr olds) - but in saying that, it was the second last question of the exam and perhaps the teacher just wanted to give the students something to work on while the others finished the easier questions. This would make some sense I suppose.

 

[Lnewqban]

The diagram you've constructed makes the similarity visually clear. I named the triangles CDB and EBA for this purpose.

A statement comparing areas could have made the problem more interesting.
For example: "Consider the area of triangle CDB to be twice the area of triangle EBA."

 

[phinds]

I believe that the diagram has been drawn out of proportion on purpose in order to induce the confusion that I suffered after just a superficial analysis.