Solve [ASK] Limit of Cosine: How to?

[Monoxdifly]

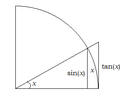
How to solve \(\displaystyle \lim_{x\rightarrow\frac{\pi}{2}}\frac{\cos{x}}{x-\frac{\pi}{2}}\)? At first I tried to convert cos x to \(\displaystyle \frac{\tan{x}}{\sin{x}}\) but then realized that \(\displaystyle \lim_{x\rightarrow c}\frac{\tan{x}}{x}\) only applies if c = 0. So, how?

 

[MarkFL]

Let's use the substitution:

\(\displaystyle u=\frac{\pi}{2}-x\)

What does the limit become then?

 

[Monoxdifly]

\(\displaystyle \lim_{u\rightarrow0}\frac{\cos{(\frac{\pi}{2}-u)}}{-u}\)?

 

[MarkFL]

\(\displaystyle \lim_{u\rightarrow0}\frac{\cos{(\frac{\pi}{2}-u)}}{-u}\)?

Yes, and so I would factor the negative sign in the denominator out in front of the limit, and apply a co-function identity to the numerator...(Thinking)

 

[Monoxdifly]

Won't it give \(\displaystyle \frac{0}{0}\) again in the \(\displaystyle \frac{\cos{\frac{\pi}{2}}\cdot\cos{u}}{u}\) part?

 

[MarkFL]

Won't it give \(\displaystyle \frac{0}{0}\) again in the \(\displaystyle \frac{\cos{\frac{\pi}{2}}\cdot\cos{u}}{u}\) part?

Recall the co-function identity:

\(\displaystyle \cos\left(\frac{\pi}{2}-\theta\right)=\sin(\theta)\)

And so our limit becomes:

\(\displaystyle L=-\lim_{u\to0}\left(\frac{\sin(u)}{u}\right)\)

And yes, this is an indeterminate form, but it is well-known to students and usually allowed as a result to use:

\(\displaystyle \lim_{x\to0}\left(\frac{\sin(x)}{x}\right)=1\)

 

[Monoxdifly]

Oops... Sorry sorry... Totally forgot about that...

 

[MarkFL]

Consider the following diagram of the unit circle in the first quadrant:

View attachment 6091

From this, we can see that for $0\le x\le\dfrac{\pi}{2}$ we have:

\(\displaystyle \sin(x)\le x\le\tan(x)\)

Dividing though by $\sin(x)$, we obtain:

\(\displaystyle 1\le\frac{x}{\sin(x)}\le\frac{1}{\cos(x)}\)

or:

\(\displaystyle \cos(x)\le\frac{\sin(x)}{x}\le1\)

And so we must then have:

\(\displaystyle \lim_{x\to0}\left(\cos(x)\right)\le\lim_{x\to0}\left(\frac{\sin(x)}{x}\right)\le\lim_{x\to0}(1)\)

or:

\(\displaystyle 1\le\lim_{x\to0}\left(\frac{\sin(x)}{x}\right)\le1\)

Hence (by the squeeze theorem):

\(\displaystyle \lim_{x\to0}\left(\frac{\sin(x)}{x}\right)=1\)