Solve Banked Curve Homework: Find Theta Given Radius, Speed, and Mass

[wmrunner24]

Homework Statement

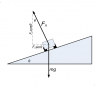
A curve of radius 52.4 m is banked so that a car traveling with uniform speed 55 km/hr
can round the curve without relying on friction to keep it from slipping to its left or right.
The acceleration of gravity is 9.8 m/s2 . The mass of the car is 1800kg.
What is θ?
Answer in units of ◦.

Homework Equations

F=ma
F_g=mgsinѲ
F_n=mgcosѲ
F_c=ma_c=mv^2/r

The Attempt at a Solution

So, the basic problem I'm having here is that I do not know what the centripetal force is. There's no friction. There may be a degree of normal force, and I'm not entirely sure if gravity is relevant. Ultimately, I know I will have to identify the centripetal force in terms of theta and other givens, then solve for theta. Any help to get there?

 

[tiny-tim]

hi wmrunner24!

… So, the basic problem I'm having here is that I do not know what the centripetal force is. There's no friction.

there is no centripetal force

there are only the usual forces, and the acceleration, so use F = ma in the usual way

 

[collinsmark]

F=ma

That's Newton's second law. So far so good.

F_g=mgsinѲ
F_n=mgcosѲ

The above two equations are not formulated correctly for this problem.

Start with a free body diagram. This is a particularly important problem to draw a free body diagram. What are the two forces acting on the car? What is the resultant force?

So, the basic problem I'm having here is that I do not know what the centripetal force is.

There is enough information given in the problem statement for you to solve this. You even posted the relevant equation for centripetal force. (All the relevant variables are given in the problem statement.)

There's no friction. There may be a degree of normal force,

Yes, that's right!

and I'm not entirely sure if gravity is relevant.

Gravity ends up being relevant. The car does not accelerate vertically. So what does that tell you about the vertical component of the normal force?

Whatever the case, start with a free body diagram. Things should become more clear after that.

 

[wmrunner24]

So then, I'm not really sure where to begin. The vertical component of the normal force must equal the force of gravity, and the horizontal component must be the centripetal force. Is that correct?

 

[collinsmark]

The vertical component of the normal force must equal the force of gravity, and the horizontal component must be the centripetal force. Is that correct?

That's a good start.

 

[wmrunner24]

So, we know then that:

F_g=F_ny (y-component of normal force)
F_c=F_nx (x-component of normal force)

From there, by way of the Pythagorean Theorem, we know:

√(F_nx^2+F_ny^2)=Fn

Substitution:

√(F_c^2+F_g^2)=Fn

√([v^2m/r]^2+[mg]^2)=Fn

√([v^2m/r]^2+[mg]^2)=mgcosѲ

Is this logic right?

If so, then all I would have to do is solve for theta.

Right?

EDIT:
I plugged this into my calculator, and it spat it back as undefined. So, clearly, this can't be the right answer if arccosine can't match an angle to the ratio.

What's wrong with this solution, and how do I get to the correct solution?

 

[collinsmark]

Not quite. It can be quite a bit simpler than that.

But first let me correct an error again. Your previous post implies that F_n = mgcosθ. That's not true!

Like you mentioned/implied in post #4, mg is equal (and opposite in direction) to a component of F_n. That's the correct way of looking at it.

But in your previous post, you're implying that F_n is a component of mg. But that's not right. It's the other way around. You have your trig function attached to the wrong term. Look at your free body diagram and it should become more clear.

Beyond that, you don't need to use the Pythagorean theorem for this problem. Work with components for now.

What is the vertical component of F_n in terms of F_n and θ? Set that equal to mg.

What is the horizontal component of F_n in terms of F_n and θ? That's the resultant force. Set that equal to the known centripetal force.

Then combine the equations (such that F_n disappears) and solve for θ.

 

[wmrunner24]

Hmm...so why isn't mgcosѲ=F_n? I was under the impression that that was the formula for the portion of the normal force caused by gravity, and to me it seemed there was only gravity here to induce normal force...except, of course, that the centripetal force would also contribute to the normal force. Is that why mgcosѲ is incorrect then?

At any rate, following what you said, we're back at:

F_g=F_ny
F_c=F_nx

Using the trig ratio is a little confusing to me. I understand how to follow what you said to finish the problem if I can identify this correctly.

So, here I've redone my free body diagram slightly, relabeling F_nx F_ny and F_n. Here, there is an unknown angle under the car of the right triangle formed, and the sine of this angle times the normal force will give F_ny and the cosine times the normal force will give F_nx. This is not theta though.

However, this angle is included in a third right triangle formed in this problem. So there is a 90 degree angle, the unnamed angle, and theta. The unknown angle must be equal to 90-Ѳ
then.

So:
F_g=F_nsin(90-Ѳ)
F_c=F_ncos(90-Ѳ)

Then solve for theta.

I'm willing to bet this is wrong. It's the best idea I had though. Sorry, I'm just not quite seeing it yet.

 

[collinsmark]

Hmm...so why isn't mgcosѲ=F_n? I was under the impression that that was the formula for the portion of the normal force caused by gravity, and to me it seemed there was only gravity here to induce normal force

Hypothetically, if you had a block on a incline that was sliding down the incline, the normal force would be F_n = mgcosθ in that case. But that's completely different from the situation in this problem.

...except, of course, that the centripetal force would also contribute to the normal force. Is that why mgcosѲ is incorrect then?

In a nutshell, yes.

So, here I've redone my free body diagram slightly, relabeling F_nx F_ny and F_n. Here, there is an unknown angle under the car of the right triangle formed, and the sine of this angle times the normal force will give F_ny and the cosine times the normal force will give F_nx. This is not theta though.

Actually, one of the angles is theta.

However, this angle is included in a third right triangle formed in this problem. So there is a 90 degree angle, the unnamed angle, and theta. The unknown angle must be equal to 90-Ѳ
then.

So:
F_g=F_nsin(90-Ѳ)
F_c=F_ncos(90-Ѳ)

To make it a little easier, realize that sin(90 - θ) = cosθ. cos(90 - θ) = sinθ.

I'm willing to bet this is wrong. It's the best idea I had though. Sorry, I'm just not quite seeing it yet.

Take a look at my free body diagram attached here.

Do you see where the F_ncosθ and F_nsinθ come from?

 

[wmrunner24]

Yeah, I see it. At first I didn't get how you identified theta, but when I sat down and looked at the geometry behind it, I figured it out.

So I'm good now, right?

Thanks a bunch for the help. My physics teacher is rather poor at explaining things, so this has been lifesaving.

 

[collinsmark]

So I'm good now, right?

I think so.

Using the above relationships you can create two equations; one corresponding to the vertical direction and the other the horizontal direction. Eventually you can combine these equations (such that F_n goes away) and solve for theta.

There is one more basic trigonometric definition that you will need in the process, but you probably already know it anyway. That relationship is:

tanθ = sinθ/cosθ.